题目内容
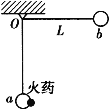
【题目】如图所示，小球a、b用等长细线悬挂于同一固定点O。让球a静止下垂，将球b向右拉起，使细线拉直水平，已知细线长为L，小球a、b的质量分别为2m和m，在小球a上固定有极少量火药。从静止释放球b，两球碰撞后火药发生爆炸而相互分开，此后观察到系小球a的细线与竖直方向之间的最大偏角为90°。忽略空气阻力，重力加速度为g，求：
(1)系小球b的细线与竖直方向之间的最大偏角；
(2)两球在碰撞过程中增加的机械能。
【答案】(1)90°；(2)2mgL
【解析】
(1)b球下摆过程中，由动能定理得
解得
碰后观察到系小球a的细线与竖直方向之间的夹角为90°，由动能定理得
解得
碰撞过程动量守恒，规定向左为正方向，由动量守恒定律可
解得
方向水平向右；
b球反向弹回，由动能定理得
解得
所以系小球b的细线与竖直方向之间的最大倾角为90°
(2)两球从碰撞前到火药爆炸后过程中增加的机械能等于碰撞前后动能的差，则有
解得
练习册系列答案
优生乐园系列答案
新编小学单元自测题系列答案
相关题目
