��Ŀ����
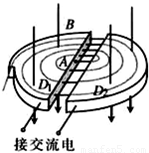
��ͼ��ʾΪ������������ԭ��ʾ��ͼ������IJ������������÷dz�����D�κУ����зֱ��һ��Ƶ������Դ������������������Ƶ��Դ�ĵ�ѹΪU����ǿ�ų��ֲ�����D�κ����Ҵ�ֱD�κ�����ƽ�棬�Ÿ�Ӧǿ��ΪB����D�κ�����S�㴦��������Դ������Դ�ų�����Ϊm��������Ϊq�����ӣ������ӵij��ٶ�Ϊ�㣩���������������٣���D�κе����뾶ΪR��������
A�����Ӹ�Ƶ�������Ƶ��Ӧ��
| ||
B�������뿪�������Ķ�����
| ||
C�������뿪������ǰ�����ٵĴ���Ϊ
| ||
D�������ڻ������������˶���ʱ��Ϊ
|

A��������
ʱ�䣬�ı�һ�η���
=
=
��f=
����A����
B���뾶ΪRʱ��qvB=
��v=
��E=
mv2=
����B����
C��һ�μ���ΪqU�������n�Σ���nqU=E��n=
����C����
D������n�Σ����˶�
�ʸ����ڣ���ʱ��
T=
=
����D��ȷ��
��ѡD
| T |
| 2 |
| T |
| 2 |
| 1 |
| 2f |
| ��m |
| qB |
| qB |
| 2��m |
B���뾶ΪRʱ��qvB=
| mv2 |
| R |
| qBR |
| m |
| 1 |
| 2 |
| B2q2R2 |
| 2m |
C��һ�μ���ΪqU�������n�Σ���nqU=E��n=
| B2qR2 |
| 2mU |
D������n�Σ����˶�
| n |
| 2 |
| n |
| 2 |
| B2qR2 |
| 4m |
| 2��m |
| qB |
| ��BR2 |
| 2U |
��ѡD

��ϰ��ϵ�д�
 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�
�����Ŀ
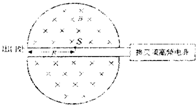
 ��ͼ��ʾΪ������������ԭ��ʾ��ͼ������IJ���������D�κУ����зֱ��һ��Ƶ������Դ��������������Ƶ��Դ�ĵ�ѹΪU����ǿ�ų���ֱD�κ�ƽ�棬�Ÿ�Ӧǿ��ΪB����D�κ�����s�㴦��������Դ��������Դ�ų�����Ϊm��������Ϊq�����ӣ������ӵij��ٶ�Ϊ0����Ȼ�������������٣���D�κе����뾶ΪR��������
��ͼ��ʾΪ������������ԭ��ʾ��ͼ������IJ���������D�κУ����зֱ��һ��Ƶ������Դ��������������Ƶ��Դ�ĵ�ѹΪU����ǿ�ų���ֱD�κ�ƽ�棬�Ÿ�Ӧǿ��ΪB����D�κ�����s�㴦��������Դ��������Դ�ų�����Ϊm��������Ϊq�����ӣ������ӵij��ٶ�Ϊ0����Ȼ�������������٣���D�κе����뾶ΪR��������A�����Ӹ�Ƶ�������Ƶ��Ӧ��
| ||
B�����Ӹ�Ƶ�������Ƶ��Ӧ��
| ||
C�������뿪������ǰ�����ٵĴ���Ϊ
| ||
D�������뿪������ʱ�Ķ�����
|
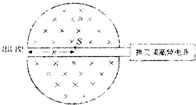 ��ͼ��ʾΪ������������ԭ��ʾ��ͼ������IJ������������÷dz�����D�κУ����зֱ��һ��Ƶ������Դ������������������Ƶ��Դ�ĵ�ѹΪU����ǿ�ų��ֲ�����D�κ����Ҵ�ֱD�κ�����ƽ�棬�Ÿ�Ӧǿ��ΪB����D�κ�����S�㴦��������Դ������Դ�ų�����Ϊm��������Ϊq�����ӣ������ӵij��ٶ�Ϊ�㣩���������������٣���D�κе����뾶ΪR��������
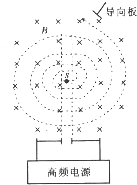
��ͼ��ʾΪ������������ԭ��ʾ��ͼ������IJ������������÷dz�����D�κУ����зֱ��һ��Ƶ������Դ������������������Ƶ��Դ�ĵ�ѹΪU����ǿ�ų��ֲ�����D�κ����Ҵ�ֱD�κ�����ƽ�棬�Ÿ�Ӧǿ��ΪB����D�κ�����S�㴦��������Դ������Դ�ų�����Ϊm��������Ϊq�����ӣ������ӵij��ٶ�Ϊ�㣩���������������٣���D�κе����뾶ΪR��������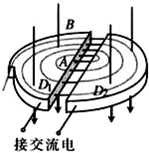 ��ͼ��ʾΪ������������ʾ��ͼ��������������D�ͽ��������ɣ�����D�κ����м俪��һ�����죬����D�ͺд�����ǿ�ų��в����ڸ�Ƶ�����Դ�ϣ���D1������A��������Դ����������������a���ӣ��������ѹ���ٺ���D2���У��ڴų������������˶����Բ�ܺ��ٴξ������ѹ���٣�Ϊ��֤����ÿ�ξ������춼�����٣��跨ʹ�����ѹ�����������������켰�ų����˶�������һ�£�����ܶ���ʼ���ٶ�Խ��Խ���˶��뾶ҲԽ��Խ�����D�ͺеı�Ե��������ٶȱ���������֪a���ӵ����Ϊq������Ϊm������ʱ�缫���ѹ��С��ΪU���ų��ĴŸ�Ӧǿ��ΪB��D�ͺеİ뾶ΪR���������խ������ͨ�������ʱ����Ժ��Բ��ƣ���a���Ӵ�����Դ����ʱ�ij��ٶ�Ϊ�㣮������a������������
��ͼ��ʾΪ������������ʾ��ͼ��������������D�ͽ��������ɣ�����D�κ����м俪��һ�����죬����D�ͺд�����ǿ�ų��в����ڸ�Ƶ�����Դ�ϣ���D1������A��������Դ����������������a���ӣ��������ѹ���ٺ���D2���У��ڴų������������˶����Բ�ܺ��ٴξ������ѹ���٣�Ϊ��֤����ÿ�ξ������춼�����٣��跨ʹ�����ѹ�����������������켰�ų����˶�������һ�£�����ܶ���ʼ���ٶ�Խ��Խ���˶��뾶ҲԽ��Խ�����D�ͺеı�Ե��������ٶȱ���������֪a���ӵ����Ϊq������Ϊm������ʱ�缫���ѹ��С��ΪU���ų��ĴŸ�Ӧǿ��ΪB��D�ͺеİ뾶ΪR���������խ������ͨ�������ʱ����Ժ��Բ��ƣ���a���Ӵ�����Դ����ʱ�ij��ٶ�Ϊ�㣮������a������������