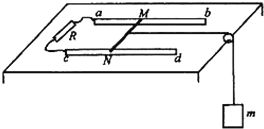
��Ŀ����
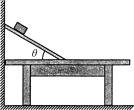
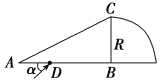
����Ŀ����ͼ��ʾ��ij�����ɽ���Ϊֱ�������ε���������뾶ΪR��![]() Բ��������ͬ��������������ɣ���֪������BC�ߵij���ΪR����BAC��30��.����һϸ����ɫ���AB���Ͼ�A��Ϊ
Բ��������ͬ��������������ɣ���֪������BC�ߵij���ΪR����BAC��30��.����һϸ����ɫ���AB���Ͼ�A��Ϊ![]() R��D������AB�߳�����45��б�����Ϸ��ķ������䣬���߾�AC�߷����պ��ܴ�ֱ��BC�߽���
R��D������AB�߳�����45��б�����Ϸ��ķ������䣬���߾�AC�߷����պ��ܴ�ֱ��BC�߽���![]() Բ������
Բ������
��1���Լ�����ߴ�Բ���ϵ�E��(ͼ��δ����)���ʱ������ǣ�
��2���Լ����ϸ�����ڲ����д�����ʱ��(��������е��ٶ�Ϊc)��
���𰸡���1��45����2��![]()
��������
��1����������������![]() Բ���еĹ�·ͼ��ͼ��ʾ��
Բ���еĹ�·ͼ��ͼ��ʾ��
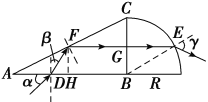
�ɼ��ι�ϵ��֪������30�����������䶨�ɿɵøò����Ըõ�ɫ���������Ϊn��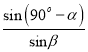
���n�� ![]()
�ɼ��ι�ϵ��֪��
![]()
������GEB�У��ɼ��ι�ϵ�ɵá�GEB��30��
����Ϊn�� ![]() ����sin ����nsin��GEB��
����sin ����nsin��GEB��![]()
������45��
��2���ɼ��ι�ϵ��֪ ![]()
�ʹ��ڲ����еĴ���·��Ϊ![]()
���ڸò����еĴ����ٶ�Ϊv��![]()
�ʹ��ڲ����д�����ʱ��Ϊt��![]()
���![]()

��ϰ��ϵ�д�
�����Ŀ