题目内容
甲乙两辆汽车在平直的公路上沿同一方向做匀变速直线运动,t = 0时刻同时经过公路旁的同一路标,下表是每隔1s记录的两车的速率。关于两车的运动,下列说法正确的是 
| A.乙车的速度变化率较大 |
| B.在 0~4s内,乙车的平均速度较大 |
| C.在 0~4s内,甲车相对乙车行驶了 56m |
| D.在乙车追上甲车之前,t=5 s时两车相距最远 |
D
解析试题分析:由表中数据知:甲车速度的变化率2m/s2,乙车速度变化率1m/s2,故甲车的速度变化率较大,选项A 错误;在 0~4s内,两车均做匀变速运动,平均速度等于中间时刻的瞬时速度,即甲车的平均速度14m/s,乙车的平均速度5m/s,故甲的平均速度较大,选项B错误;在 0~4s内,甲的位移为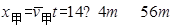 ,乙的位移:
,乙的位移: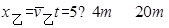 ,故甲车相对乙车行驶了36m,选项C错误;t=5 s时两车,两车的速度均为8m/s,故此时两车距离最远,选项D 正确;
,故甲车相对乙车行驶了36m,选项C错误;t=5 s时两车,两车的速度均为8m/s,故此时两车距离最远,选项D 正确;
考点:匀变速运动的规律;追击问题。

 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案列车长为l,铁路桥长为2l,列车匀加速行驶过桥,车头过桥头的速度为v1,车头过桥尾时的速度为v2,则车尾过桥尾时速度为( )
| A.3v2-v1 | B.3v2+v1 | C. | D. |
一物体在外力的作用下从静止开始做直线运动,合外力方向不变,大小随时间的变化如图所示。设该物体在t0和2t0时刻相对于出发点的位移分别是x1和x2,速度分别是v1和v2,合外力从开始至t0时刻做的功是W1,从t0至2t0时刻做的功是W2,则( )
| A.x2 = 5x1 v2 = 3v1 | B.x1 = 9x2 v2 = 5v1 |
| C.x2 = 5x1 W2 = 8W1 | D.v2 = 3v1 W2 = 9W1 |
小球沿足够长的斜面向上做匀变速运动,依次经a、b、c、d到达最高点e。已知ab=bd=6 m,bc=1 m,小球从a到c和从c到d所用的时间都是2 s,设小球经b、c时的速度分别为vb、vc,则( ) 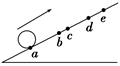
A.vc= m/s m/s | B.vb=3m/s |
| C.ce=9 m | D.从d到e所用时间为4 s |
如图所示,竖直平面内的轨道Ⅰ和Ⅱ都由两段细直杆连接而成,两轨道长度相等。用相同的水平恒力将穿在轨道最低点的B静止小球,分别沿Ⅰ和Ⅱ推至最高点A,所需时间分别为t1、t2;动能增量分别为 、
、 。假定球在经过轨道转折点前后速度的大小不变,且球与Ⅰ、Ⅱ轨道间的动摩擦因数相等,则
。假定球在经过轨道转折点前后速度的大小不变,且球与Ⅰ、Ⅱ轨道间的动摩擦因数相等,则
A. > > ;t1>t2 ;t1>t2 | B. = = ;t1>t2 ;t1>t2 |
C. > > ;t1<t2 ;t1<t2 | D. = = ;t1<t2 ;t1<t2 |
汽车以20 m/s的速度做匀速直线运动,刹车的加速度大小为5 m/s2,那么开始刹车后2 s内与开始刹车后6 s内汽车通过的位移之比为
| A.1∶1 | B.1∶3 | C.3∶4 | D.4∶3 |


 算得g值,则其中
算得g值,则其中 的值(已记入表中),作出
的值(已记入表中),作出

 s
s