题目内容
8.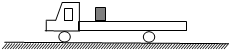 如图所示,一木箱静止、在长平板车上,某时刻平板车以a=2.5m/s2的加速度由静止开始向前做匀加速直线运动,当速度达到v=9m/s时改做匀速直线运动,己知木箱与平板车之间的动摩擦因数μ=0.225,箱与平板车之间的最大静摩擦力与滑动静擦力相等(g取10m/s2).求:
如图所示,一木箱静止、在长平板车上,某时刻平板车以a=2.5m/s2的加速度由静止开始向前做匀加速直线运动,当速度达到v=9m/s时改做匀速直线运动,己知木箱与平板车之间的动摩擦因数μ=0.225,箱与平板车之间的最大静摩擦力与滑动静擦力相等(g取10m/s2).求:(1)车在加速过程中木箱运动的加速度的大小
(2)木箱做加速运动的时间和位移的大小
(3)要使木箱不从平板车上滑落,木箱开始时距平板车右端的最小距离.
分析 (1)根据牛顿第二定律求出木箱的最大加速度,判断出木箱与平板车发生相对滑动,从而得出木箱运动的加速度大小.
(2)根据速度时间公式求出木箱加速的时间,结合速度位移公式 求出木箱加速的位移.
(3)根据运动学公式求出木箱和平板车速度相同时两者的位移大小,从而求出木箱开始时距平板车右端的最小距离.
解答 解:(1)设木箱的最大加速度为a′,根据牛顿第二定律μmg=ma′,
解得a′=2.25m/s2<2.5m/s2.
则木箱与平板车存在相对运动,所以车在加速过程中木箱的加速度为2.25m/s2.
(2)设木箱的加速时间为t1,加速位移为x1.${t_1}=\frac{v}{a'}=\frac{9m/s}{{2.25m/{s^2}}}=4s$
${x_1}=\frac{v^2}{2a'}=\frac{9^2}{2×2.25}=18m$
(3)设平板车做匀加速直线运动的时间为t2,则${t_2}=\frac{v}{a}=\frac{9}{2.5}=3.6s$
达共同速度平板车的位移为x2则${x_2}=\frac{v^2}{2a}+v({t_1}-{t_2})=\frac{9^2}{2×2.5}+9×(4-3.6)=19.8m$
要使木箱不从平板车上滑落,木箱距平板车末端的最小距离满足△x=x1-x2=19.8-18=1.8m
答:(1)车在加速过程中木箱运动的加速度的大小为2.25m/s2.
(2)木箱做加速运动的时间为4s,位移的大小为18m.
(3)木箱开始时距平板车右端的最小距离为1.8m.
点评 本题关键正确分析平板车和货箱的运动情况,明确他们之间的位移、速度关系,根据运动学公式列方程求解.

练习册系列答案
相关题目
18.关于运动的合成和分解,下列说法正确的是(
| A. | 合运动的时间等于两个分运动的时间之和 | |
| B. | 合速度一定比其中一个分速度大 | |
| C. | 合运动的加速度不可能与分运动的加速度相同 | |
| D. | 两个互成角度的初速度不为零的匀变速直线运动的合运动可能是直线运动 |
3.研究表明,地球自转在逐渐变慢,3亿年前地球自转的周期约为22小时.假设这种趋势会持续下去,而地球的质量保持不变,未来人类发射的地球同步卫星与现在的相比( )
| A. | 线速度变小 | B. | 角速度变大 | ||
| C. | 向心加速度变大 | D. | 距地面的高度变小 |
1.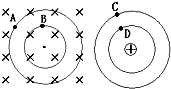 四个荷质比相等的点电荷A、B、C、D,A、B在匀强磁场中做匀速圆周运动,C、D绕点电荷做匀速圆周运动,A、C和B、D的半径分别相等,若A、C的线速度均为V,则关于B、D的线速度VB、VD的大小,正确的说法是( )
四个荷质比相等的点电荷A、B、C、D,A、B在匀强磁场中做匀速圆周运动,C、D绕点电荷做匀速圆周运动,A、C和B、D的半径分别相等,若A、C的线速度均为V,则关于B、D的线速度VB、VD的大小,正确的说法是( )
 四个荷质比相等的点电荷A、B、C、D,A、B在匀强磁场中做匀速圆周运动,C、D绕点电荷做匀速圆周运动,A、C和B、D的半径分别相等,若A、C的线速度均为V,则关于B、D的线速度VB、VD的大小,正确的说法是( )
四个荷质比相等的点电荷A、B、C、D,A、B在匀强磁场中做匀速圆周运动,C、D绕点电荷做匀速圆周运动,A、C和B、D的半径分别相等,若A、C的线速度均为V,则关于B、D的线速度VB、VD的大小,正确的说法是( )| A. | VD>VB>V | B. | VD>V>VB | C. | VB=VD>V | D. | VD<V<VB |
18.假设人造卫星绕地球做匀速圆周运动,当卫星绕地球运动的轨道半径增大到原来的2倍仍作圆周运动,则( )
| A. | 根据公式v=ωr,可知卫星的线速度将增大到原来的2倍 | |
| B. | 根据公式F=m$\frac{v^2}{r}$,可知卫星所需的向心力将减少到原来的$\frac{1}{2}$ | |
| C. | 根据公式F=G$\frac{Mm}{r^2}$,可知卫星所需的向心力将减少到原来的$\frac{1}{4}$ | |
| D. | 根据B和C中给出的公式,可知卫星运动的线速度将减少到原来的$\frac{{\sqrt{2}}}{2}$ |
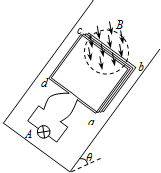 如图所示,粗糙斜面的倾角θ=37°,半径r=0.5m的圆形区域内存在着垂直于斜面向下的匀强磁场.一个匝数n=10匝的刚性正方形线框abcd,通过松弛的柔软导线与一个额定功率P=1.25W的小灯泡A相连,圆形磁场的一条直径恰好过线框bc边.已知线框质量m=2kg,总电阻R0=1.25Ω,边长L>2r,与斜面间的动摩擦因数μ=0.5.从t=0时起,磁场的磁感应强度按B=2-$\frac{2}{π}$t(T)的规律变化.开始时线框静止在斜面上,在线框运动前,灯泡始终正常发光.设最大静摩擦力等于滑动摩擦力,g取10m/s2,sin37°=0.6,cos37°=0.8.求:
如图所示,粗糙斜面的倾角θ=37°,半径r=0.5m的圆形区域内存在着垂直于斜面向下的匀强磁场.一个匝数n=10匝的刚性正方形线框abcd,通过松弛的柔软导线与一个额定功率P=1.25W的小灯泡A相连,圆形磁场的一条直径恰好过线框bc边.已知线框质量m=2kg,总电阻R0=1.25Ω,边长L>2r,与斜面间的动摩擦因数μ=0.5.从t=0时起,磁场的磁感应强度按B=2-$\frac{2}{π}$t(T)的规律变化.开始时线框静止在斜面上,在线框运动前,灯泡始终正常发光.设最大静摩擦力等于滑动摩擦力,g取10m/s2,sin37°=0.6,cos37°=0.8.求: 如图所示是一段光导纤维的简化图,光纤总长为L,已知光从左端射入光线在光纤的侧面上恰好能发生全反射.若已知该光纤的折射率为n,光在真空中传播速度为c,求:
如图所示是一段光导纤维的简化图,光纤总长为L,已知光从左端射入光线在光纤的侧面上恰好能发生全反射.若已知该光纤的折射率为n,光在真空中传播速度为c,求: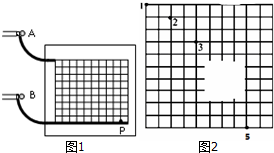 如图1所示,两个完全相同的圆弧轨道分别固定在竖直板上的不同高度处,轨道的末端水平,在它们相同位置上各安装一个电磁铁,两个电磁铁由同一个开关控制,通电后,两电磁铁分别吸住相同小铁球A、B,断电后,两个小球同时开始运动.离开圆弧轨道后,A球做平抛运动,B球进入一个光滑的水平轨道,则:
如图1所示,两个完全相同的圆弧轨道分别固定在竖直板上的不同高度处,轨道的末端水平,在它们相同位置上各安装一个电磁铁,两个电磁铁由同一个开关控制,通电后,两电磁铁分别吸住相同小铁球A、B,断电后,两个小球同时开始运动.离开圆弧轨道后,A球做平抛运动,B球进入一个光滑的水平轨道,则: