题目内容
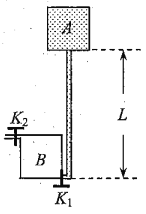
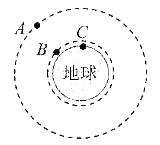
【题目】如图所示，A是地球的同步卫星，B是地球的近地卫星，C是地面上的物体，A、B、C质量相等，均在赤道平面上绕地心做匀速圆周运动。设A、B与地心连线在单位时间内扫过的面积分别为SA、SB，周期分别为TA、TB、TC，A、B、C做圆周运动的动能分别为EkA、EkB、EkC。不计A、B、C之间的相互作用力，下列关系式正确的是（ ）
A. SA=SB
B. SA＞SB
C. TA=TB＜TC
D. EkA＜EkB=EkC
【答案】B
【解析】赤道上的物体A与同步通信卫星C转动周期相同，即
，根据
，由于赤道上物体C的轨道半径小于同步通信卫星A的轨道半径，故
，根据动能
，A与C的质量相等，而，故
；A、B是围绕地球公转的卫星，根据
，得线速度
，周期
，因A的轨道半径大于B的轨道半径，则有
，根据，A与B的质量相等，而
，故
，人造卫星绕地球做匀速圆周运动的圆的面积为：
，所以人造卫星与地心连线在单位时间内所扫过的面积为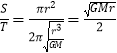
，因A的轨道半径大于B的轨道半径，则有
，综上分析可得：
，
，，故ACD错误，B正确；故选B.
练习册系列答案
阅读快车系列答案
相关题目
