题目内容
 (2013?商丘三模)如图所示,在固定的光滑水平杆(杆足够长)上,套有一个质量为m=0.5kg的光滑金属圆环,轻绳一端拴在环上,另一端系着一个质量为M=1.98kg的木块,现有一质量为m0=20g的子弹以v0=100m/s的水平速度射入木块并留在木块中(不计空气阻力和子弹与木块作用的时间,g取10m/s2),求:
(2013?商丘三模)如图所示,在固定的光滑水平杆(杆足够长)上,套有一个质量为m=0.5kg的光滑金属圆环,轻绳一端拴在环上,另一端系着一个质量为M=1.98kg的木块,现有一质量为m0=20g的子弹以v0=100m/s的水平速度射入木块并留在木块中(不计空气阻力和子弹与木块作用的时间,g取10m/s2),求:①圆环、木块和子弹这个系统损失的机械能;
②木块所能达到的最大高度.
分析:①子弹射穿木块的过程遵守动量守恒,由动量守恒定律求出子弹穿出木块后子弹和木块的共同速度.即可求得系统损失的机械能;
②木块向右摆动的过程中,圆环向右滑动,此过程中,系统水平方向不受外力,水平方向的动量守恒.当两者水平速度相同时向右摆到最大高度,由系统的水平方向动量守恒求出和机械能守恒结合求解木块向右摆动的最大高度.
②木块向右摆动的过程中,圆环向右滑动,此过程中,系统水平方向不受外力,水平方向的动量守恒.当两者水平速度相同时向右摆到最大高度,由系统的水平方向动量守恒求出和机械能守恒结合求解木块向右摆动的最大高度.
解答:解:①子弹射入木块过程,系统的动量守恒,取向右方向为正方向,根据动量守恒定律得:
则有:m0v0=(m0+M)v
得:v=
=
m/s=1m/s
机械能只在该过程有损失,损失的机械能为
△E=
m0
-
(m0+M)v2=[
×0.02×1002-
×(0.02+1.98)×12]J=99J
②木块(含子弹)在向上摆动过程中,以木块(含子弹)和圆环木块(含子弹)和圆环组成的系统为研究对象,根据系统水平方向的动量守恒得,
则有:(m0+M)v=(m0+M+m)v'
解得:v'=
=
m/s=0.8m/s
根据机械能守恒定律有:
(m0+M)v2=
(m0+M+m)v′2+(m0+M)gh
联立解得:
h=
=
m=0.01m
答:①圆环、木块和子弹这个系统损失的机械能为99J;
②木块所能达到的最大高度为0.01m.
则有:m0v0=(m0+M)v
得:v=
| m0v0 |
| m0+M |
| 0.02×100 |
| 0.02+1.98 |
机械能只在该过程有损失,损失的机械能为
△E=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
②木块(含子弹)在向上摆动过程中,以木块(含子弹)和圆环木块(含子弹)和圆环组成的系统为研究对象,根据系统水平方向的动量守恒得,
则有:(m0+M)v=(m0+M+m)v'
解得:v'=
| (m0+M)v |
| m0+M+m |
| (0.02+1.98)×1 |
| 0.02+1.98+0.5 |
根据机械能守恒定律有:
| 1 |
| 2 |
| 1 |
| 2 |
联立解得:
h=
| ||||
| (m0+M)g |
| ||||
| (0.02+1.98)×10 |
答:①圆环、木块和子弹这个系统损失的机械能为99J;
②木块所能达到的最大高度为0.01m.
点评:本题是连接体机械能守恒和水平方向动量守恒问题,关键要正确选择研究对象,明确研究的过程.此题研究只能针对系统,对单个物体机械能不守恒.

练习册系列答案
相关题目
 (2013?商丘三模)如图,MN和PQ是电阻不计的平行金属导轨,其间距为L,导轨弯曲部分光滑,平直部分粗糙,右端接一个阻值为R的定值电阻.平直部分导轨左边区域有宽度为d、方向竖直向上、磁感应强度大小为B的匀强磁场.质量为m、电阻也为R的金属棒从高为h处静止释放,到达磁场右边界处恰好停止.已知金属棒与平直部分导轨间的动摩擦因数为u,金属棒与导轨间接触良好.则金属棒穿过磁场区域的过程中( )
(2013?商丘三模)如图,MN和PQ是电阻不计的平行金属导轨,其间距为L,导轨弯曲部分光滑,平直部分粗糙,右端接一个阻值为R的定值电阻.平直部分导轨左边区域有宽度为d、方向竖直向上、磁感应强度大小为B的匀强磁场.质量为m、电阻也为R的金属棒从高为h处静止释放,到达磁场右边界处恰好停止.已知金属棒与平直部分导轨间的动摩擦因数为u,金属棒与导轨间接触良好.则金属棒穿过磁场区域的过程中( ) (2013?商丘三模)质点做直线运动的位移x和时间平方t2的关系图象如图所示,则该质点( )
(2013?商丘三模)质点做直线运动的位移x和时间平方t2的关系图象如图所示,则该质点( )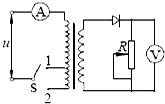 (2013?商丘三模)一台理想变压器,开始时开关S接1,此时原、副线圈的匝数比是11:1,原线圈接入电压为220V的正弦交流电.一只理想二级管和一个滑动变阻器串联接在副线圈上,如图所示.则下列判断正确的是( )
(2013?商丘三模)一台理想变压器,开始时开关S接1,此时原、副线圈的匝数比是11:1,原线圈接入电压为220V的正弦交流电.一只理想二级管和一个滑动变阻器串联接在副线圈上,如图所示.则下列判断正确的是( )