题目内容
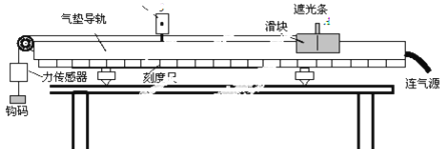
【题目】将一轻质弹簧水平放置，一段固定在A点，另一端与质量为m=0.1 kg的物块P接触但不连接。AB是水平轨道，B端与半径为R=0.4 m的光滑半圆轨道BCD相切，半圆的直径BD竖直。用外力推动P压缩弹簧，然后放开，物块P开始沿着轨道运动，物块P恰能通过最高点D。重力加速度为g=10 m/s2，求：
(1)物块在D点的速度；
(2)物块通过圆弧轨道上B点时对轨道的压力。
(3)若弹簧原长时右端的位置与B点的距离L=4 m，动摩擦因数μ=0.2，其余部分光滑。计算物块离开弹簧的过程中，弹簧弹力的冲量。
【答案】（1）2 m/s （2）6N （3）0.6kg·m/s
【解析】试题分析：物块P恰好能够到达D点时，由重力提供向心力，由牛顿第二定律求出D点的速度；从B到D，由机械能守恒定律列式，可求出物体P在B点的速度．再由牛顿运动定律求物块通过圆弧轨道上B点时对轨道的压力，根据动量定理，即可求得弹簧弹力的冲量。
物块P恰好通过D点，由重力提供向心力，由牛顿第二定律可得： 
解得： 
=2 m/s
对物块P从B点运动到D点过程中，
动能定理： 
在B点由牛顿第二定律可得： 
根据第三定律得压力F=FN，即F=6mg=6N 方向向下
物块离开弹簧到B点，根据动能定理： 
代入数据解得：v0=6m/s
根据动量定理，弹簧弹力的冲量I=mv0-0=0.6kg·m/s
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
