题目内容
18. A、B两金属板如图竖直固定在绝缘底座上,与底座的总质量为1kg.将其静止放在光滑水平面上,已知两金属板间接电源的电压恒为U=1280V,极板间距为d=6.4m,在A板底端上有一孔.在距A板0.8m处有质量为1kg和2kg不带电的物体m、M处于静止,M在右(如图),物体m、M与底座的动摩擦因素都为0.5,物体m、M放有少量炸药(炸药的质量不计),炸药有48J化学能转化为系统的动能,物体M从右端A板上的孔滑出,物体m与B金属板发生完全弹性碰撞且带上0.1C的正电荷.物体m、M视质点,g=10m/s2.
A、B两金属板如图竖直固定在绝缘底座上,与底座的总质量为1kg.将其静止放在光滑水平面上,已知两金属板间接电源的电压恒为U=1280V,极板间距为d=6.4m,在A板底端上有一孔.在距A板0.8m处有质量为1kg和2kg不带电的物体m、M处于静止,M在右(如图),物体m、M与底座的动摩擦因素都为0.5,物体m、M放有少量炸药(炸药的质量不计),炸药有48J化学能转化为系统的动能,物体M从右端A板上的孔滑出,物体m与B金属板发生完全弹性碰撞且带上0.1C的正电荷.物体m、M视质点,g=10m/s2.(1)炸药爆炸后的瞬间物体m、M的速度
(2)物体M从右端A板上的孔滑出的速度
(3)物体m从右端A板上的孔滑出的速度.
分析 (1)在爆炸的过程中,两个物块组成的系统的动量守恒,结合动能的表达式即可求出两个物块的速度;
(2)对M和底座分别进行受力分析,结合牛顿第二定律与运动学的公式即可求出;
(3)M滑出后,m与底座组成的系统的动量守恒定律,应用运动学的公式与牛顿第二定律求出碰撞前的速度,然后应用动量守恒定律与功能关系即可求出碰撞后的速度,最后由运动学的公式与牛顿第二定律即可求出物体m从右端A板上的孔滑出的速度.
解答 解:(1)选择向右为正方向,在爆炸的过程中,两个物块组成的系统的动量守恒,得:
Mv1+mv2=0
又:$\frac{1}{2}m{v}_{2}^{2}+\frac{1}{2}M{v}_{1}^{2}=48$J
联立得:v1=-8m/s;v2=4m/s
(2)m与底座之间的摩擦力:f1=μmg=0.5×1×10=5N
M与底座之间的摩擦力:f2=μMg=0.5×2×10=10N
M对底座的摩擦力向右,M对底座的摩擦力向左,所以底座受到的合力的大小是:F底座=f2-f1=10-5=5N,方向向右,所以底座将向右做匀加速直线运动.
底座的加速度:${a}_{1}=\frac{{F}_{底座}}{{m}_{0}}=\frac{5}{1}=5m/{s}^{2}$
M的加速度:${a}_{M}=-\frac{{f}_{2}}{M}=-\frac{10}{2}=-5m/{s}^{2}$
M向右左匀减速运动,底座向右左匀加速直线运动,设经过时间t1物体M从右端A板上的孔滑出,则:${v}_{2}{t}_{1}+\frac{1}{2}{a}_{M}{t}_{1}^{2}-\frac{1}{2}{a}_{底座}{t}_{1}^{2}=l$
代入数据得:t1=0.4s
物体M从右端A板上的孔滑出的速度:vM=v2+aMt1
代入数据得:vM=2m/s
此过程中,m的加速度:${a}_{m}=\frac{{f}_{1}}{m}=\frac{5}{1}=5m/{s}^{2}$,
可知m向左做匀减速直线运动,位移:$x′={v}_{1}{t}_{1}+\frac{1}{2}{a}_{m}{t}_{1}^{2}$
代入数据得:x′=-2.8m,
底座的位移:x=$\frac{1}{2}{a}_{底座}{t}_{1}^{2}=\frac{1}{2}×5×0.{4}^{2}=0.8$m
可知物块m还没有与底座的挡板发生碰撞.
(3)物体M从右端A板上的孔滑出时底座的速度:v3=a底座t1=5×0.4=2m/s
m的速度:v1′=v1+amt1=-8+5×0.4=-6m/s
此后,m受到的摩擦力的方向仍然向右,继续做匀减速直线运动,而底座则只受到向左的摩擦力的作用,加速度的方向边为向左,所以:
${a}_{底座}′=-\frac{{f}_{1}}{{m}_{0}}=-\frac{5}{1}=-5m/{s}^{2}$
设再经过时间t2二者相碰,二者的相对位移:$△x=d-l-x-|\begin{array}{l}{x′}\\{\;}\end{array}|=6.4-0.8-0.8-2.8=2$m
又:$△x=|\begin{array}{l}{{v}_{1}′{t}_{2}+\frac{1}{2}{a}_{m}{t}_{2}^{2}}\\{\;}\end{array}|+{v}_{3}{t}_{2}+\frac{1}{2}{a}_{底座}′{t}_{2}^{2}$
代入数据得:${t}_{2}=\frac{4-\sqrt{6}}{5}≈0.31$s(另一个解$\frac{4+\sqrt{6}}{5}$不符合题意,舍去)
则碰撞前m的速度:v1″=v1′+amt2=-6+5×0.31=-4.45m/s
底座的速度:v3′=v3+a底座′t2=2+(-5)×0.31=0.45m/s
物体m与B金属板发生完全弹性碰撞的过程中因同时满足动量守恒定律与能量守恒定律,设碰撞后m的速度为v4,底座的速度为v5,得:
mv1″+m0v3′=mv4+m0v5
$\frac{1}{2}mv{″}_{1}^{2}+\frac{1}{2}{m}_{0}v{′}_{3}^{3}=\frac{1}{2}m{v}_{4}^{2}+\frac{1}{2}{m}_{0}{v}_{5}^{2}$
联立得:v4=0.45m/s;v5=-4.45m/s
由图可知,电场的方向由B向A,即向右,所以m受到的电场力的方向向右,大小:${F}_{电}=qE=\frac{qU}{d}=\frac{0.1×1280}{6.4}=20$N
由于m相对于底座向右运动,所以受到的摩擦力的方向向左,同时底座受到的摩擦力的方向向右.
m受到的合力:Fm=F电-f1=20-5=15N
加速度:$a=\frac{{F}_{m}}{m}=\frac{15}{1}=15$m/s2
底座的加速度:$a′=\frac{{f}_{1}}{{m}_{0}}=\frac{5}{1}=5m/{s}^{2}$
设经过t3物体m从右端A板上的孔滑出,则:
L=${v}_{4}{t}_{3}+\frac{1}{2}a{t}_{3}^{2}$+$|\begin{array}{l}{{v}_{5}{t}_{3}+\frac{1}{2}a′{t}_{3}^{2}}\\{\;}\end{array}|$
代入数据得:t3=0.74s
则物体m从右端A板上的孔滑出的速度:v6=v4+at3=0.45+15×0.74=11.55m/s
答:(1)炸药爆炸后的瞬间物体m的速度大小是8m/s,方向向左,M的速度大小是4m/s,方向向右;
(2)物体M从右端A板上的孔滑出的速度是2m/s;
(3)物体m从右端A板上的孔滑出的速度是11.55m/s.
点评 本题综合考查了动量守恒定律、能量守恒定律和动能定理,涉及的过程多,力的变化复杂,综合性较强,对学生的能力要求较高,需加强这方面的训练.

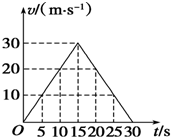 下表是通过测量得到的一辆摩托车沿直线做加速运动时的速度随时间的变化.
下表是通过测量得到的一辆摩托车沿直线做加速运动时的速度随时间的变化.| t/s | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| v/ (m•s-1) | 0 | 10 | 20 | 30 | 20 | 10 | 0 |
(1)求摩托车在第一个10s内的加速度.
(2)求摩托车在最后15s内的加速度.
(3)求摩托车在总过程中的位移.
| A. | 研究小木块得翻倒过程 | |
| B. | 研究从桥上通过的一列队伍 | |
| C. | 研究在推力作用下沿竖直方向运动的火箭 | |
| D. | 在研究汽车后轮牵引力来源的时候 |
| A. | 研究汽车通过某一路标所用的时间 | |
| B. | 做精彩表演的花样滑冰运动员 | |
| C. | 研究火车通过某山洞时的位移 | |
| D. | 计算汽车从天津开到北京所用的时间 |
| A. | 41N 0 | B. | 41N 11N | C. | 29N 4N | D. | 41N lN |
| A. | 牛顿第一定律 | B. | 牛顿第二定律 | C. | 牛顿第三定律 | D. | 机械能守恒定律 |
 如图所示,直线MN上方有垂直于纸面向外的足够大的有界匀强磁场区域,磁感应强度为B,正、负电子同时从O点与MN成30°角的相同速度v射入该磁场区域(电子质量为m,电荷量为e),经一段时间后从边界MN射出,求:
如图所示,直线MN上方有垂直于纸面向外的足够大的有界匀强磁场区域,磁感应强度为B,正、负电子同时从O点与MN成30°角的相同速度v射入该磁场区域(电子质量为m,电荷量为e),经一段时间后从边界MN射出,求: