题目内容
5. 如图1所示,在某星球表面轻绳约束下的质量为m的小球在竖直平面内做圆周运动,小球在最低点与最高点所受轻绳的拉力之差为△F,假设星球是均匀球体,其半径为R,已知万有引力常量为G.不计一切阻力.
如图1所示,在某星球表面轻绳约束下的质量为m的小球在竖直平面内做圆周运动,小球在最低点与最高点所受轻绳的拉力之差为△F,假设星球是均匀球体,其半径为R,已知万有引力常量为G.不计一切阻力.(1)求星球表面重力加速度;
(2)求该星球的密度;
(3)如图2所示.在该星球表面上,某小球以大小为v0的初速度平抛,恰好能击中倾角为θ的斜面,且位移最短.试求该小球平抛的时间.
分析 (1)在最高点,重力和拉力的合力提供向心力,根据牛顿第二定律列式;最低点,拉力和重力的合力提供向心力,再次根据牛顿第二定律列式;再根据动能定理列式;最后联立求解即可;
(2)在星球表面,重力等于万有引力,根据万有引力定律列式求解;
(3)位移最短,说明位移方向与斜面垂直,根据平抛运动的规律列式求解.
解答 解:(1)在最高点,重力和拉力的合力提供向心力,故:${F}_{1}+mg=m\frac{{v}_{1}^{2}}{R}$
再最低点,重力和拉力的合力提供向心力,故:${F}_{2}-mg=m\frac{{v}_{2}^{2}}{R}$
根据动能定理,有:$mg(2R)=\frac{1}{2}m{v}_{2}^{2}-\frac{1}{2}m{v}_{1}^{2}$
联立解得:F2-F1=6mg
根据题意,有:小球在最低点与最高点所受轻绳的拉力之差为△F,故:g=$\frac{△F}{6m}$
(2)在星球表面,重力等于万有引力,故:
m′g=G$\frac{m′M}{{R}^{2}}$
$ρ=\frac{M}{\frac{4}{3}π{R}^{3}}$
联立解得:
ρ=$\frac{△F}{8πmR}$
(3)位移最短,说明位移方向与斜面垂直,故位移偏转角为($\frac{π}{2}$-θ),故:
tan($\frac{π}{2}$-θ)=$\frac{y}{x}$
y=$\frac{1}{2}g{t}^{2}$
x=v0t
联立解得:
t=$\frac{{12m{v_0}}}{△Ftanθ}$
答:(1)星球表面重力加速度为$\frac{△F}{6m}$;
(2)该星球的密度为$\frac{△F}{8πmR}$;
(3)该小球平抛的时间为$\frac{{12m{v_0}}}{△Ftanθ}$.
点评 本题是竖直平面内的圆周运动问题、平抛运动问题、万有引力定律问题的综合,涉及规律多,关键是区分各个运动模型的动力学规律.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 物体的初速度是5m/s | B. | 物体的加速度大小是5m/s2 | ||
| C. | 物体的初速度是10m/s | D. | 物体的加速度大小是2.5m/s2 |
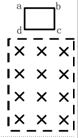 如图所示,闭合矩形线圈abcd从静止开始竖直下落,穿过一个匀强磁场区域,磁场长度远大于线圈长度,不计空气阻力,则此线圈从cd边进入磁场到ab边穿出磁场为止,以下说法中正确的是( )
如图所示,闭合矩形线圈abcd从静止开始竖直下落,穿过一个匀强磁场区域,磁场长度远大于线圈长度,不计空气阻力,则此线圈从cd边进入磁场到ab边穿出磁场为止,以下说法中正确的是( )| A. | 始终有一向下的速度 | B. | 一定有一向下的加速度 | ||
| C. | 加速度可能为零 | D. | 加速度可能向上 |
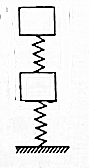
| A. | 弹簧k1在上,物块M在上 | B. | 弹簧k1在上,物块m在上 | ||
| C. | 弹簧k2在上,物块M在上 | D. | 弹簧k2在上,物块m在上 |
| A. | 导体对电流的阻碍作用叫做导体的电阻,因此只有导体中有电流通过时才有电阻 | |
| B. | 由R=$\frac{U}{I}$可知导体的电阻与导体两端的电压成正比,跟导体中的电流成反比 | |
| C. | 由公式R=p$\frac{l}{S}$可知,导体的电阻率与导体的电阻Rx导体的长度l和横截面积S有关 | |
| D. | 金属导体的电阻率不仅与导体的材料有关,而且还随着温度的变化而变化 |
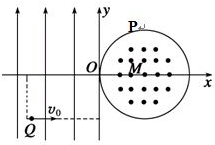 如图所示,在平面直角坐标系xOy内,第二、三象限内存在沿y轴正方向的匀强电场,第一、四象限内存在半径为L的圆形匀强磁场,磁场方向垂直于坐标平面向外.一个质量 为m,带电量为q的带正电的粒子从第三象限中的Q(-2L,-L)点以速度v0沿x轴正方向射出,恰好从坐标原点O进入磁场,从P(2L,0)点射出磁场.不计粒子重力,求:
如图所示,在平面直角坐标系xOy内,第二、三象限内存在沿y轴正方向的匀强电场,第一、四象限内存在半径为L的圆形匀强磁场,磁场方向垂直于坐标平面向外.一个质量 为m,带电量为q的带正电的粒子从第三象限中的Q(-2L,-L)点以速度v0沿x轴正方向射出,恰好从坐标原点O进入磁场,从P(2L,0)点射出磁场.不计粒子重力,求: 如图所示是某质点直线运动的v-t图象,请回答:
如图所示是某质点直线运动的v-t图象,请回答: