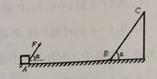题目内容
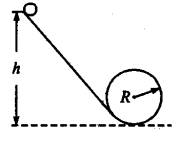
一质量m＝2kg的小球从光滑斜面上高h=3．5m处由静止滑下，斜面底端紧接着一个半径R=1m的光滑圆环(如图)．求：
(1)小球滑至圆环顶点时对环的压力．
(2)小球至少应从多高处静止滑下才能越过圆环最高点？
(3)小球从h′＝2m处静止滑下时将在何处脱离圆环(g＝10m／s2)？
答案：
解析：
提示：
解析：
(1)40N (2)2．5 m (3)q＝arccos
|
，
角是球与圆心连线与竖直方向的夹角提示：
提示：(1)小球在顶点时受力如图，据牛顿第二定律N＋G＝m A→B据机械能守恒，取最低点为零势能面有： mgh＝mg2R＋ ①②联立得：N′＝N＝40N． (2)当vB有最小值时即mg＝m h最小，再据机械能守恒定律mgh＝mg2R＋ 得h＝2．5m． (3)设在如图C点脱离圆环，此时小球只受重力，据牛顿第二定律mgcosq＝m 又A→C据机械能守恒定律有： mgh′＝mg(R＋Rcosq)＋ ①②联立得q＝arccos
|
mvＢ2
②
mvＢ2
①
mvＣ2 ②
(
角如图)．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
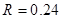m的半圆轨道最低点P的切线相平。现有一质量m＝2kg的滑块（可视为质点）以
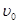＝6m/s的初速度滑上小车左端，二者共速时小车还未与墙壁碰撞，当小车与墙壁碰撞时即被粘在墙壁上，已知滑块与小车表面的滑动摩擦因数μ＝0.2，g取10m/s2．
，小物块与水平面间的动摩擦因数
，水平面与斜面之间B点有一小段弧形连接，一质量m＝2kg的小物块静止于A点，现用与水平方向成
到达B点，并迅速撤去拉力F。A、B两点相距
，（已知
，
，g取
），求：
；
