题目内容
18.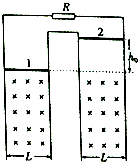 如图所示,竖直平面内有足够长、不计电阻的两组平行光滑金属导轨,宽度均为L=0.5m,上方连接一个R=2Ω的定值电阻,虚线下方的区域内存在垂直纸面向内、磁感应强度B=2T的匀强磁场.完全相同的两根金属杆1和2靠在导轨上,金属杆与导轨等宽且与导轨接触良好,电阻均为r=1Ω.将金属杆1固定在磁场的上边缘(仍在此磁场内),金属杆2从磁场边界上方h0=0.8m处由静止释放,进入磁场后恰做匀速运动.(g取10m/s2).
如图所示,竖直平面内有足够长、不计电阻的两组平行光滑金属导轨,宽度均为L=0.5m,上方连接一个R=2Ω的定值电阻,虚线下方的区域内存在垂直纸面向内、磁感应强度B=2T的匀强磁场.完全相同的两根金属杆1和2靠在导轨上,金属杆与导轨等宽且与导轨接触良好,电阻均为r=1Ω.将金属杆1固定在磁场的上边缘(仍在此磁场内),金属杆2从磁场边界上方h0=0.8m处由静止释放,进入磁场后恰做匀速运动.(g取10m/s2).(1)金属杆的质量m为多大?
(2)若金属杆2从磁场边界上方h1=0.2m处由静止释放,进入磁场经过一段时间后开始匀速运动.此过程中电阻R产生的热量为0.7J,求金属杆2在磁场中下落的高度h2以及在此过程中通过金属杆横截面的电荷量q;
(3)若金属杆2从离磁场边界上方h3处静止释放,同时静止释放金属杆1.当金属杆1速度为1m/s时,金属杆2恰好进入磁场,要使金属杆1和金属杆2立刻做匀速运动,则金属杆2的释放高度h3应该为多大?
分析 (1)金属杆2进入磁场前做自由落体运动,由运动学公式求出进入磁场时的速度v,进入磁场后做匀速运动,重力与安培力平衡,E=BLv,I=$\frac{E}{R+2r}$、F=BIL,及平衡条件可求得m.
(2)金属杆2进入磁场经过一段时间后开始匀速运动,速度大小仍等于v.根据能量守恒求出h2,由$\overline{E}$=$\frac{△Φ}{△t}$,$\overline{I}$=$\frac{\overline{E}}{R+2r}$,q=$\overline{I}$•t2求出电量q.
(3)由平衡关系可求得电流大小;再由两棒切割磁感线产生的电动势,由欧姆定律求解速度,再由自由落体规律可求得下落的高度.
解答 解:(1)金属杆2进入磁场前做自由落体运动
由${v}_{m}^{2}$=2gh0得金属杆2进入磁场时的速度vm=$\sqrt{2gh0}$=4 m/s;
金属杆2进入磁场后受力平衡:mg=BIL
且E=BLvm,I=$\frac{E}{2r+R}$
解得:$m=\frac{{B}^{2}{L}^{2}{v}_{m}}{(2r+R)g}$
解得:m=0.1kg
(2)设金属杆2刚进入磁场时的速度为v
v2=2gh1
解得v=$\sqrt{2g{h}_{1}}$=2 m/s
金属杆2进入磁场到匀速运动的过程中,设金属杆2在磁场内下降h2.
此过程中,电阻R、金属杆1和金属杆2串联,电流相等.故回路中产生的热量:Q=$\frac{2r+R}{R}{Q}_{R}$=1.4J
由能量守恒定律有:$mg({h}_{1}+{h}_{2})=\frac{1}{2}m{v}_{m}^{2}$+Q
解得h2=1.3m
又$\overline{E}$=$\frac{BL{h}_{2}}{{t}_{2}}$
因电磁感应定律,$\overline{I}$=$\frac{\overline{E}}{R+2r}$,
且q=$\overline{I}t$
得:$q=\frac{BL{h}_{2}}{R+2r}$=$\frac{2×0.5×1.3}{1+2×0.5}$=0.65C
(3)设金属杆2进入磁场时,金属杆1和2的速度分别为v1、v2,两杆受力情况相同,所以要使它们匀速下落,则有:mg=BIL
而电路中的电流I=$\frac{E′}{R+2r}$
两金属杆切割所产生的电动势E'=E1+E2=BLv1+BLv2
联立解得:v2=$\frac{mg(R+2r)}{{B}^{2}{L}^{2}}$-v1;
解得:v2=3m/s;
根据自由落体规律可得:h3=$\frac{{v}_{2}^{2}}{2g}$
解得:h3=0.45m;
答:(1)金属杆的质量m为0.1kg;
(2)在此过程中通过金属棒横截面的电荷量为0.65C;
(3)金属杆2的释放高度h3应该为0.45m.
点评 本题是电磁感应与力学知识的综合,第3问关键是抓住两杆的加速度相同,任何时刻速度的增量相同这一隐含的条件分析两杆的速度关系.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案| A. | 1.25×103m3 | B. | 1.25×106m3 | C. | 2.5×106m3 | D. | 5×108m3 |
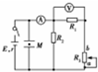 如图所示,平行金属板中带电质点M原来处于静止状态,不考虑电流表和电压表对电路的影响,当滑动变阻器R3的滑片向b端移动时,下列说法正确的是( )
如图所示,平行金属板中带电质点M原来处于静止状态,不考虑电流表和电压表对电路的影响,当滑动变阻器R3的滑片向b端移动时,下列说法正确的是( )| A. | 电源的内电压增大,电压表读数增大 | |
| B. | 电路中的总电阻增大,电流表读数减小 | |
| C. | 外电压增大,质点M将向上运动 | |
| D. | R1消耗的功率减小,R2消耗的功率增大 |

| A. | u2=350sin(50πt)V | |
| B. | u2=350cos(100πt)V | |
| C. | 为使用户电压稳定在220V,应将P适当下移 | |
| D. | 为使用户电压稳定在220V,应将P适当上移 |



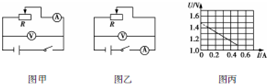 在测量电源电动势与内阻的实验中,有如下实验器材:
在测量电源电动势与内阻的实验中,有如下实验器材: