题目内容
6.一个质量为m的小球距地平面的高度为H,把小球以水平速度为$\sqrt{gH}$水平抛出,以地平面为参考平面,求小球速度为落地速度的$\frac{2}{3}$时的重力势能.分析 小球运动过程中机械能守恒,对小球从抛出到落地与从抛出到速度为落地速度的$\frac{2}{3}$过程分别列式,即可求解.
解答 解:设小球落地时速度大小为v.小球速度为落地速度的$\frac{2}{3}$时的重力势能为Ep.
根据机械能守恒得:
mgH+$\frac{1}{2}m(\sqrt{gH})^{2}$=$\frac{1}{2}m{v}^{2}$;
mgH+$\frac{1}{2}m(\sqrt{gH})^{2}$=Ep+$\frac{1}{2}m(\frac{2}{3}v)^{2}$
联立得:Ep=$\frac{5}{6}$mgH
答:小球速度为落地速度的$\frac{2}{3}$时的重力势能为$\frac{5}{6}$mgH.
点评 解决本题的关键要灵活选择研究的过程,运用机械能守恒定律列式解答.

练习册系列答案
相关题目
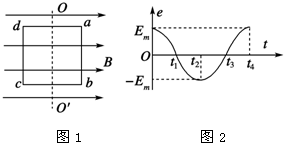
16.如图1一矩形线圈,绕垂直于匀强磁场并位于线圈平面的固定轴转动,线圈中的感应电动势e随时间t的变化如图2,下列说法中正确的是( )

| A. | t1时刻通过线圈的磁通量为零 | |
| B. | t2时刻线圈位于中性面 | |
| C. | t3时刻通过线圈的磁通量变化率的绝对值最大 | |
| D. | 每当e变化方向时,通过线圈的磁通量最大 |
17.行星绕恒星的运动轨道近似为圆形,行星的运行周期T的平方与轨道半径R的三次方的比$\frac{{T}^{2}}{{R}^{3}}$为常数后,则常数的大小( )
| A. | 只跟行星的质量有关 | |
| B. | 只跟恒星的质量有关 | |
| C. | 跟恒星的质量及行量的质量都有关系 | |
| D. | 跟恒星的质量及行星的质量都没关系 |
14.用跨过定滑轮的绳把湖中小船拉靠岸,如图所示,已知拉绳的速度v0保持不变,则船速( )


| A. | 保持不变 | B. | 逐渐增大 | C. | 逐渐减小 | D. | 先增大后减小 |
18. 在xOy坐标系中Ⅰ、Ⅳ象限有垂直纸面向里的匀强磁场,a、b两个相同带电粒子(重力不计),从x轴上点M(L,0)以相同速率v同时在xQy平面内向不同方向发射,其中a沿+y方向,经磁场偏转后,两粒子先后到达y轴上的点N(0,$\sqrt{3}L$),根据以上信息,可以求出的物理量有( )
在xOy坐标系中Ⅰ、Ⅳ象限有垂直纸面向里的匀强磁场,a、b两个相同带电粒子(重力不计),从x轴上点M(L,0)以相同速率v同时在xQy平面内向不同方向发射,其中a沿+y方向,经磁场偏转后,两粒子先后到达y轴上的点N(0,$\sqrt{3}L$),根据以上信息,可以求出的物理量有( )
 在xOy坐标系中Ⅰ、Ⅳ象限有垂直纸面向里的匀强磁场,a、b两个相同带电粒子(重力不计),从x轴上点M(L,0)以相同速率v同时在xQy平面内向不同方向发射,其中a沿+y方向,经磁场偏转后,两粒子先后到达y轴上的点N(0,$\sqrt{3}L$),根据以上信息,可以求出的物理量有( )
在xOy坐标系中Ⅰ、Ⅳ象限有垂直纸面向里的匀强磁场,a、b两个相同带电粒子(重力不计),从x轴上点M(L,0)以相同速率v同时在xQy平面内向不同方向发射,其中a沿+y方向,经磁场偏转后,两粒子先后到达y轴上的点N(0,$\sqrt{3}L$),根据以上信息,可以求出的物理量有( )| A. | a、b粒子各自转过的圆心角 | B. | a、b粒子到达N点的时间差 | ||
| C. | 磁感应强度B的大小 | D. | 粒子的比荷 |


 水平U形光滑框架,宽度为1m,电阻忽略不计,导体棒ab的质量m=0.2kg、电阻R=0.5Ω,匀强磁场的磁感应强度B=0.2T,方向垂直框架向上.现用F=1N的外力由静止开始向右拉ab棒,当ab棒的速度达到2m/s时,求:
水平U形光滑框架,宽度为1m,电阻忽略不计,导体棒ab的质量m=0.2kg、电阻R=0.5Ω,匀强磁场的磁感应强度B=0.2T,方向垂直框架向上.现用F=1N的外力由静止开始向右拉ab棒,当ab棒的速度达到2m/s时,求: