题目内容
18. 在xOy坐标系中Ⅰ、Ⅳ象限有垂直纸面向里的匀强磁场,a、b两个相同带电粒子(重力不计),从x轴上点M(L,0)以相同速率v同时在xQy平面内向不同方向发射,其中a沿+y方向,经磁场偏转后,两粒子先后到达y轴上的点N(0,$\sqrt{3}L$),根据以上信息,可以求出的物理量有( )
在xOy坐标系中Ⅰ、Ⅳ象限有垂直纸面向里的匀强磁场,a、b两个相同带电粒子(重力不计),从x轴上点M(L,0)以相同速率v同时在xQy平面内向不同方向发射,其中a沿+y方向,经磁场偏转后,两粒子先后到达y轴上的点N(0,$\sqrt{3}L$),根据以上信息,可以求出的物理量有( )| A. | a、b粒子各自转过的圆心角 | B. | a、b粒子到达N点的时间差 | ||
| C. | 磁感应强度B的大小 | D. | 粒子的比荷 |
分析 根据洛伦兹力提供向心力,使其做匀速圆周运动,并由题意可分劣圆弧与优圆弧,从而由几何关系来确定已知长度与半径的关系,并由周期公式可两个粒子到达B点的时间差.
解答  解:作出ab的运动的轨迹如图
解:作出ab的运动的轨迹如图
对于a的运动轨迹,由几何关系得:${R}^{2}=(R-L)^{2}+(\sqrt{3}L)^{2}$
解得:R=2L
a粒子的偏转角:$sinθ=\frac{\sqrt{3}L}{2L}=\frac{\sqrt{3}}{2}$,所以$θ=\frac{1}{3}π$.
同理,由图可得b粒子的偏转角:$β=\frac{5}{3}π$.
a粒子在磁场中运动的时间:${t}_{A}=\frac{θR}{v}=\frac{πR}{3v}$=$\frac{2πL}{3v}$,
b粒子在磁场中运动的时间:${t}_{B}=\frac{βR}{v}=\frac{5πR}{3v}=\frac{10πL}{3v}$,
所以,它们到达B点的时间差:$△t={t}_{B}-{t}_{A}=\frac{8πL}{3v}$.故A、B正确.
粒子的轨迹半径可以求出,但是比荷无法得知,所以也无法求出磁感应强度,故C、D错误.
故选:AB.
点评 该题的关键是根据题意,正确画出ab两个粒子运动的轨迹,并能够得出它们运动的时间的关系.常规题目.

练习册系列答案
相关题目
8.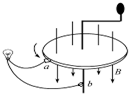 法拉第发明了世界上第一台发电机--法拉第圆盘发电机.铜质圆盘放置在匀强磁场中,圆盘圆心处固定一个摇柄,边缘和圆心处各有一个铜电刷与其紧贴,用导线a、b将电刷与电灯连接起来形成回路.如图所示从上往下看逆时针匀速转动铜盘,若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,转动的角速度为ω.则下列说法正确的是( )
法拉第发明了世界上第一台发电机--法拉第圆盘发电机.铜质圆盘放置在匀强磁场中,圆盘圆心处固定一个摇柄,边缘和圆心处各有一个铜电刷与其紧贴,用导线a、b将电刷与电灯连接起来形成回路.如图所示从上往下看逆时针匀速转动铜盘,若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,转动的角速度为ω.则下列说法正确的是( )
 法拉第发明了世界上第一台发电机--法拉第圆盘发电机.铜质圆盘放置在匀强磁场中,圆盘圆心处固定一个摇柄,边缘和圆心处各有一个铜电刷与其紧贴,用导线a、b将电刷与电灯连接起来形成回路.如图所示从上往下看逆时针匀速转动铜盘,若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,转动的角速度为ω.则下列说法正确的是( )
法拉第发明了世界上第一台发电机--法拉第圆盘发电机.铜质圆盘放置在匀强磁场中,圆盘圆心处固定一个摇柄,边缘和圆心处各有一个铜电刷与其紧贴,用导线a、b将电刷与电灯连接起来形成回路.如图所示从上往下看逆时针匀速转动铜盘,若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,转动的角速度为ω.则下列说法正确的是( )| A. | 回路中的电动势等于BL2ω | |
| B. | 回路中的电流等于$\frac{{B{L^2}ω}}{2R}$ | |
| C. | 回路中电流方向从b导线流进灯泡,a导线流进铜盘 | |
| D. | 回路中产生的是大小和方向周期性变化的电流 |
13.图1是远距离输电线路的示意图,圈2是发电机输出电压随时间变化的图象,则( )


| A. | 发电机输出交流电压的有效值约为500 V | |
| B. | 用户用电器上交流电的频率是100 Hz | |
| C. | 输电线的电流只由升压变压器原副线圈的匝数比决定 | |
| D. | 当用户用电器的总电阻减小时,输电线上损失的功率增大 |
10.如图所示是一列简谐波在某一时刻的波形,则在该时刻( )


| A. | B、C两点的平衡位置间距为$\frac{λ}{4}$,即1m | |
| B. | B点的振幅最大,C点的振幅是0 | |
| C. | 经一个周期,质点从A点到达E点 | |
| D. | 如果质点B在0.35s内通过的路程为14cm,则波速为20m/s |
 如图所示,质量为m的小球用长为L的细线拴在天花板上的O点,现将小球拉开,使摆线L与竖直方向的夹角为α,并使小球在水平面内做匀速圆周运动(这种运动通常称为圆锥摆运动).求:
如图所示,质量为m的小球用长为L的细线拴在天花板上的O点,现将小球拉开,使摆线L与竖直方向的夹角为α,并使小球在水平面内做匀速圆周运动(这种运动通常称为圆锥摆运动).求: 光滑金属导轨宽L=0.4m,电阻不计,均匀变化的磁场穿过整个轨道平面,如图甲所示.磁场的磁感应强度随时间变化的情况如图乙所示.金属棒ab的电阻为1Ω,自t=0时刻起从导轨最左端以v0=1m/s的速度向右匀速运动,则1秒末回路中的电动势为1.6V,此时ab棒所受磁场力为1.28N.
光滑金属导轨宽L=0.4m,电阻不计,均匀变化的磁场穿过整个轨道平面,如图甲所示.磁场的磁感应强度随时间变化的情况如图乙所示.金属棒ab的电阻为1Ω,自t=0时刻起从导轨最左端以v0=1m/s的速度向右匀速运动,则1秒末回路中的电动势为1.6V,此时ab棒所受磁场力为1.28N. 质量为800kg的小汽车驶过一座半径为40m的圆形拱桥,到达桥顶时的速度为10m/s.求:
质量为800kg的小汽车驶过一座半径为40m的圆形拱桥,到达桥顶时的速度为10m/s.求: