题目内容
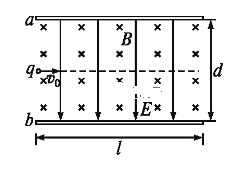
【题目】如图所示,水平放置的两块带电金属极板a、b平行正对.极板长度为l,板间距为d,板间存在着方向竖直向下、电场强度大小为E的匀强电场和垂直于纸面向里的匀强磁场.假设电场、磁场只存在于两板间.一质量为m、电荷量为q的粒子,以水平速度v0从两极板的左端正中央沿垂直于电场、磁场的方向射入极板间,恰好做匀速直线运动.不计粒子的重力及空气阻力.
（1）求匀强磁场磁感应强度B的大小;
（2）若撤去磁场,粒子能从极板间射出,求粒子穿过电场时沿电场方向移动的距离;
（3）若撤去电场，还是让该粒子以水平速度v0从两极板的左端正中央沿垂直于磁场的方向射入极板间，为使粒子不从磁场中射出，求所加磁场的磁感应强度的范围.
【答案】（1） 
（2）
（3）
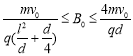
【解析】
（1）粒子做匀速直线运动，所受电场力与洛伦兹力平衡：
解得：
（2）撤去磁场，粒子在极板之间做类平抛运动，分解位移：
电场力提供加速度：
联立方程解得粒子穿过电场时沿电场方向移动的距离：
（3）撤去电场，粒子在匀强磁场中做匀速圆周运动，由于粒子的电性不影响结果，所以假设粒子带正电，则粒子的运动轨迹如图所示。
若为轨迹1，则粒子的运动半径：
洛伦兹力提供向心力：
联立方程解得：
若为轨迹2，则根据勾股定理，粒子的运动半径：
洛伦兹力提供向心力：
联立方程解得：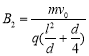
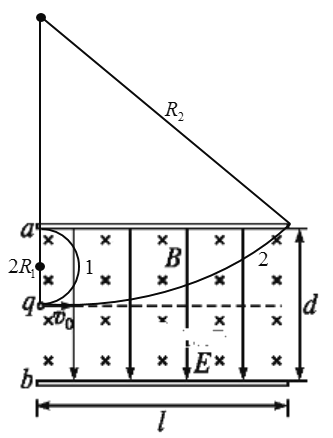
为使粒子不从磁场中射出，所加磁感应强度的范围为：
即：
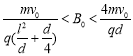
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
