题目内容
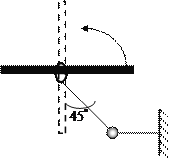
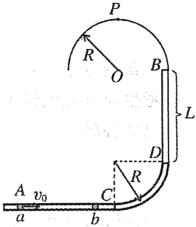
【题目】细管 AB 内壁光滑、厚度不计,加工成如图所示形状。长 L=0.5m 的 BD 段竖直,其 B 端与半径 R=0.3m 的光滑圆弧轨道平滑连接,P 点为圆弧轨道的最高点。CD 段是半径 R=0.3m 的四分之一圆弧,AC 段在水平面上。管中有两个可视为质点的小球 a、b, 质量分别为 ma=6kg、mb=2kg。最初 b 球静止在管内 AC 段某一位置,a 球以速度 v0 水平向右运动,与b 球发生弹性碰撞。重力加速度g 取10m/s2。
(1)若 v0=4m/s,求碰后 a、b 两球的速度大小:
(2)若 a 球恰好能运动到 B 点,求 v0的大小,并通过分析判断此情况下 b 球能否通过 P 点。
【答案】(1)2m/s,6m/s(2)8m/s,能。
【解析】
(1)由于 a、b 的碰撞是弹性碰撞,碰撞过程中动量守恒
mav0=mava+mbvb
同时,碰撞过程中机械能也守恒
![]()
由以上两式可解得
![]()
![]()
(2) 在 a碰撞以后的运动过程中,a小球机械能守恒。若a恰好运动到B点,即到达B点时速度为 0
![]()
解得:
v1=4m/s
由(1)问中计算可知
![]()
解得:
v0=8m/s
同理也可求出b球碰撞以后的速度
![]()
假设 b球能上到P点,上升过程中机械能守恒
![]()
解得
![]()
若恰好能运动到P点
![]()
解得:
![]()
可得 v3>vP因此,b球能够通过 P点.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目