Question

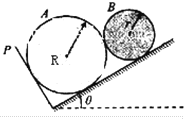
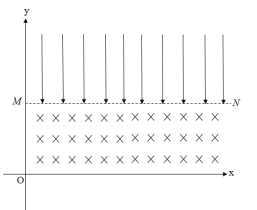
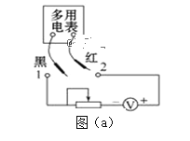
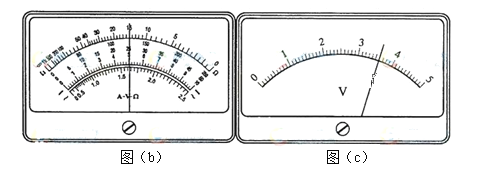
【题目】如图所示，水平放置的平行金属板AB间的距离d=0.1m，板长L=0.3m，在金属板的左端竖直放置一带有小孔的挡板，小孔恰好位于AB板的正中间，距金属板右端x=0.5m处竖直放置一足够大的荧光屏，现在AB板间加如图（b）所示周期性的方波形电压，已知U0=1.0×102V，t=0s时刻，A板电势高于B板电势。在挡板的左侧，有大量带负电的相同粒子以平行于金属板方向的速度持续射向挡板，粒子的质量m=1.0×10-7kg，电荷量q=1.0×10-2C，速度大小均为v0=1.0×104m/s，带电粒子的重力不计，则：

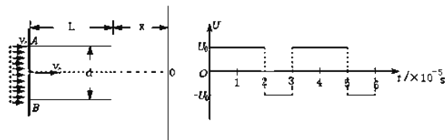
（1）求粒子在电场中的运动时间；

（2）求在t=0时刻进入的粒子打在荧光屏上的位置到光屏中心O点的距离；

（3）若撤去挡板，求粒子打在荧光屏上的最高位置和最低位置到光屏中心O点的距离。

Answer 1

【答案】(1) (2)0.85m（3）0.1m,0.005

【解析】

（1）进入电场的粒子在水平方向不受力，做匀速直线运动：L=v0t

粒子在电场中运动时间

（2）粒子在电场运动时间一共是3×10-5s，根据两极板电压变换图b，在竖直方向上0-2×10-5s粒子匀加速运动，粒子匀减速直线运动，由于电压大小一样，所以加速度大小相等
离开电场时竖直方向速度：
竖直方向位移：
离开电场后到金属板的过程，水平方向匀速直线运动：x=v0t′
竖直方向匀速直线运动y′=vyt′=0.05m
所以打到荧光屏的位置到O点的距离y+y′=0.085m

因为任意时刻进入电场的粒子在电场中运动的时间=T（交变电场变化的周期），设粒子在任意的t0时刻进入，离开电场时竖直方向的末速度 均相同 （也可借助图像分析）

所以所有粒子离开电场时的速度方向相互平行

由（2）得，t=nT （n=0、1、2...）时刻进入的粒子，离开电场时在竖直方向上具有最大的位移y=0.035m

若粒子进入的位置合适，粒子可以从极板的上边缘离开电场，如图所示；

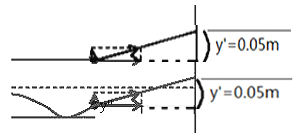
故粒子打到荧光屏上最高点到O点的的距离为

nT＋≤ t≤nT＋2T/3时刻进入的粒子，若粒子进入的位置合适，粒子向B板运动的速度减小到0时，粒子刚好可以到达B板，随后开始向A板加速，加速时间均为t=1×10-5s，此情形下粒子射出极板时位置最低，打到荧光屏上的位置也最低。对应粒子射出极板时离B板距离为
则粒子打到荧光屏上最低点到O点的的距离为0.005m。