题目内容
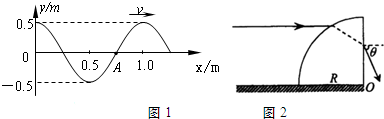
(1)有一列简谐横波在弹性介质中沿x轴正方向以速率v=10m/s传播,某时刻的波形如图1所示,该波的周期T= s;
振幅A= m.
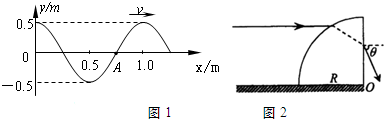
(2)一半径为R的
球体放置在水平面上,球体由折射率为
的透明材料制成.现有一束位于过球心O的竖直平面内的光线,平行于桌面射到球体表面上,折射入球体后再从竖直表面射出,如图2所示.已知入射光线与桌面的距离为
.求出射角.
振幅A=
(2)一半径为R的
| 1 |
| 4 |
| 3 |
| ||
| 2 |

分析:简谐横波是波传播方向与质点振动方向相互垂直,由图可知周期、振幅及开始运动的位置.
当光从图示位置射入,经过二次折射后射出球体,由折射定律可求出射出光线的折射角.
当光从图示位置射入,经过二次折射后射出球体,由折射定律可求出射出光线的折射角.
解答: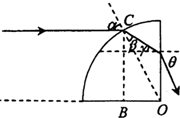 解:(1)由图可知,波的波长为1m,而波速为10m/s,由T=
解:(1)由图可知,波的波长为1m,而波速为10m/s,由T=
=
s=0.1s
则有波的周期为0.1s; 由图象可知波的振幅为0.5m.
(2)设入射光线与
球体的交点为C,连接OC,OC即为入射点的法线.
因此,图中的角α为入射角.过C点作球体水平表面的垂线,垂足为B.
依题意,∠COB=α.又由△OBC知sinα=
设光线在C点的折射角为β,由折射定律得
=
解得β=30°
由几何关系知,光线在球体的竖直表面上的入射角γ(见图)为30°.
由折射定律得
=
因此sinθ=
解得θ=60°
 解:(1)由图可知,波的波长为1m,而波速为10m/s,由T=
解:(1)由图可知,波的波长为1m,而波速为10m/s,由T=| λ |
| v |
| 1 |
| 10 |
则有波的周期为0.1s; 由图象可知波的振幅为0.5m.
(2)设入射光线与
| 1 |
| 4 |
因此,图中的角α为入射角.过C点作球体水平表面的垂线,垂足为B.
依题意,∠COB=α.又由△OBC知sinα=
| ||
| 2 |
设光线在C点的折射角为β,由折射定律得
| sinα |
| sinβ |
| 3 |
解得β=30°
由几何关系知,光线在球体的竖直表面上的入射角γ(见图)为30°.
由折射定律得
| sinγ |
| sinθ |
| 1 | ||
|
因此sinθ=
| ||
| 2 |
解得θ=60°
点评:当光线从球体入射时,法线则是入射点与球心的连线;当光线射出时,法线则与界面垂直.因此两次使用折射定律可求出结果.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 的透明材料制成。现有一束位于过球心O的竖直平面内的光线,平行于桌面射到球体表面上,折射入球体后再从竖直表面射出,如图所示。已知入射光线与桌面的距离为
的透明材料制成。现有一束位于过球心O的竖直平面内的光线,平行于桌面射到球体表面上,折射入球体后再从竖直表面射出,如图所示。已知入射光线与桌面的距离为 .求出射角。
.求出射角。

 的透明材料制成。现有一束位于过球心O的竖直平面内的光线,平行于桌面射到球体表面上,折射入球体后再从竖直表面射出,如图所示。已知入射光线与桌面的距离为
的透明材料制成。现有一束位于过球心O的竖直平面内的光线,平行于桌面射到球体表面上,折射入球体后再从竖直表面射出,如图所示。已知入射光线与桌面的距离为 .求出射角。
.求出射角。