��Ŀ����
����Ŀ����ͼ��ʾxoyƽ���ڣ�y��5cm��y��0�ķ�Χ�ڴ�����ǿ�ų����ų�����ֱֽ������Ÿ�Ӧǿ�Ⱦ�ΪB=1.0T��һ������Ϊm=1.6��10��15kg��������Ϊq=1.6��10��7C�Ĵ������ӣ�������ԭ��O��v0=5.0��105m/s���ٶ�����x���30��ǵķ���б������������ų�ƫתǡ�ô�x���ϵ�Q��ɹ�������Q��ʱ���ٶȷ���Ҳб���ϣ�������������=3.14������������3λ��Ч���֣�����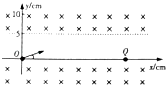
��1�����Ӵ�O���˶���Q���õ����ʱ�䣻
��2�����Ӵ�O���˶���Q�����ͨ����·�̣�
���𰸡�
��1���⣺���ӵ��˶��켣��ͼ��ʾ
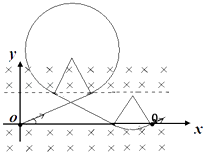
�����ӵ�һ����б���ϵ��ٶȾ���Q��ʱ��ʱ����̣��ڴų����˶�ʱ��Ϊt1���У� ![]()
�ã� ![]()
�֣� ![]()
�������ݵã�r=0.05m��T=6.28��10��7s
��ͼ��֪�������ڴų����˶���ʱ����һ�����ڣ����ԣ�
![]() s
s
���������˶���ʱ��Ϊt2���У� ![]() s
s
![]() s
s
�����Ӵ�O���˶���Q���õ����ʱ����1.028��10��6s��
��2�����ӵ��˶�������Բ��ϵ��ظ���������������ڴų��е�·��Ϊ��
s1=2n��r��n=1��2��3����
��������·��Ϊ��s2=4nd��n=1��2��3����
��·��Ϊ��s=s1+s2=0.514n��n=1��2��3����
�����Ӵ�O���˶���Q�����ͨ����·����0.514n����n=1��2��3����
����������1�������������ڴų����˶����Ȼ����˶��켣��Ȼ�� ���ݼ��ι�ϵ������ںͰ뾶��ʽ����˶�ʱ�䣬���ӵ�һ����б���ϵ��ٶȾ���Q��ʱ��ʱ����̣������ڴų����˶���ʱ�������������˶���ʱ����ӾͿ���������Ӵ�O���˶���Q���õ����ʱ�䡣
��2�����ӵ��˶����Ӧ���ǵ�һ���˶��������ظ������������Ե��˶�����һ���˶�·�̵������������һ�ε�·�̳��Դ����Ϳ����ˡ�
�����㾫�����������⣬������Ҫ�˽���������(��������ʼ�մ�ֱ��v�ķ���������������һ��������)��

 �����ܿ����ϵ�д�
�����ܿ����ϵ�д�