题目内容
(2013?普陀区一模)如图所示,两平行光滑的金属导轨MN、PQ固定在水平面上,相距为L,处于竖直向下的磁场中,整个磁场由n个宽度皆为x0的条形匀强磁场区域1、2…n组成,从左向右依次排列,磁感应强度的大小分别为B、2B、3B…nB,两导轨左端MP间接入电阻R,一质量为m的金属棒ab垂直于MN、PQ放在水平导轨上,与导轨电接触良好,不计导轨和金属棒的电阻.

(1)对金属棒ab施加水平向右的力,使其从图示位置开始运动并穿过n个磁场区,求棒穿越磁场区1的过程中通过电阻R的电量q.
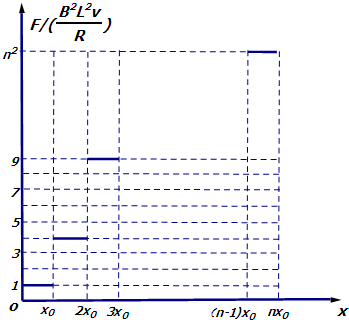
(2)对金属棒ab施加水平向右的拉力,让它从图示位置由静止开始做匀加速运动,当棒进入磁场区1时开始做匀速运动,速度的大小为v.此后在不同的磁场区施加不同的拉力,使棒保持做匀速运动穿过整个磁场区.取棒在磁场1区左边界为x=0,作出棒ab所受拉力F随位移x变化的图象.
(3)求第(2)中棒通过第i(1≤i≤n)磁场区时的水平拉力Fi和棒在穿过整个磁场区过程中回路产生的电热Q.
(用x0、B、L、m、R、n表示)


(1)对金属棒ab施加水平向右的力,使其从图示位置开始运动并穿过n个磁场区,求棒穿越磁场区1的过程中通过电阻R的电量q.
(2)对金属棒ab施加水平向右的拉力,让它从图示位置由静止开始做匀加速运动,当棒进入磁场区1时开始做匀速运动,速度的大小为v.此后在不同的磁场区施加不同的拉力,使棒保持做匀速运动穿过整个磁场区.取棒在磁场1区左边界为x=0,作出棒ab所受拉力F随位移x变化的图象.
(3)求第(2)中棒通过第i(1≤i≤n)磁场区时的水平拉力Fi和棒在穿过整个磁场区过程中回路产生的电热Q.
(用x0、B、L、m、R、n表示)

分析:(1)法拉第电磁感应定律、欧姆定律求解棒穿越磁场区1的过程中通过电阻R的电量q.
(2)当棒进入磁场区时开始做匀速运动,拉力与安培力平衡,由安培力公式FA=
,得到拉力,可作出图象.
(3)由动能定理求出棒刚进入磁场时的速度,由拉力与安培力平衡,可求得棒通过第i(1≤i≤n)磁场区时的水平拉力Fi.棒克服安培力做功,等于产生的热量,可求解总热量.
(2)当棒进入磁场区时开始做匀速运动,拉力与安培力平衡,由安培力公式FA=
| B2L2v |
| R |
| △Φ |
| R |
(3)由动能定理求出棒刚进入磁场时的速度,由拉力与安培力平衡,可求得棒通过第i(1≤i≤n)磁场区时的水平拉力Fi.棒克服安培力做功,等于产生的热量,可求解总热量.
解答:解:(1)电路中产生的感应电动势为:E=
通过电阻R的电量为:q=
△t,
=
,
得到 q=
导体棒通过I区过程:△Φ=BLx0
解得:q=
(2)当棒进入磁场区时开始做匀速运动,拉力与安培力平衡,由安培力公式FA=
,则得 拉力F=FA=
,作图如图.
(3)设进入I区时拉力为F1,速度v,则有:
F1x0=
mv 2 ①
F1=FA=
,②
联立①②解得 F1=
,v=
所以 Fi=
Q=F1x0+F2x0…+Fnx0
故Q=
(12+22+…n2)
答:(1)棒穿越磁场区1的过程中通过电阻R的电量q为
.
(2)拉力F随位移x变化的图象如图.
(3)棒通过第i(1≤i≤n)磁场区时的水平拉力Fi为 Fi=
,棒在穿过整个磁场区过程中回路产生的电热Q=
(12+22+…n2).
| △Φ |
| △t |
通过电阻R的电量为:q=
. |
| I |
. |
| I |
| ||
| R |
得到 q=
| △Φ |
| R |
导体棒通过I区过程:△Φ=BLx0
解得:q=
| BLx0 |
| R |
(2)当棒进入磁场区时开始做匀速运动,拉力与安培力平衡,由安培力公式FA=
| B2L2v |
| R |
| B2L2v |
| R |

(3)设进入I区时拉力为F1,速度v,则有:
F1x0=
| 1 |
| 2 |
F1=FA=
| B2L2v |
| R |
联立①②解得 F1=
| 2B4L4x0 |
| mR2 |
| 2B2L2x0 |
| mR |
所以 Fi=
| 2i2B4L4x0 |
| mR2 |
Q=F1x0+F2x0…+Fnx0
故Q=
2
| ||
| mR2 |
答:(1)棒穿越磁场区1的过程中通过电阻R的电量q为
| BLx0 |
| R |
(2)拉力F随位移x变化的图象如图.
(3)棒通过第i(1≤i≤n)磁场区时的水平拉力Fi为 Fi=
| 2i2B4L4x0 |
| mR2 |
2
| ||
| mR2 |
点评:对于电磁感应问题,感应电量q=
和安培力FA=
,都是常用的经验公式,在学会推导的基础上记牢,有助于分析.本题是数列问题,运用归纳法研究.
| △Φ |
| R |
| B2L2v |
| R |

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
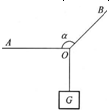 (2013?普陀区一模)如图所示,物体G用两根绳子悬挂,开始时绳OA水平,现将两绳同时沿顺时针方向转过90°,且保持两绳之间的夹角α不变(α>90°),物体保持静止状态.在旋转过程中,设绳OA的拉力为T1,绳OB的拉力为T2,则( )
(2013?普陀区一模)如图所示,物体G用两根绳子悬挂,开始时绳OA水平,现将两绳同时沿顺时针方向转过90°,且保持两绳之间的夹角α不变(α>90°),物体保持静止状态.在旋转过程中,设绳OA的拉力为T1,绳OB的拉力为T2,则( )
 (2013?普陀区一模)如图所示,AB是一根裸导线,单位长度的电阻为R0,一部分弯曲成半径为r0的圆圈,圆圈导线相交处导电接触良好.圆圈所在区域有与圆圈平面垂直的均匀磁场,磁感强度为B.导线一端B点固定,A端在沿BA方向的恒力F作用下向右缓慢移动,从而使圆圈缓慢缩小.设在圆圈缩小过程中始终保持圆的形状,导体回路是柔软的,在此过程中F所作功全部变为
(2013?普陀区一模)如图所示,AB是一根裸导线,单位长度的电阻为R0,一部分弯曲成半径为r0的圆圈,圆圈导线相交处导电接触良好.圆圈所在区域有与圆圈平面垂直的均匀磁场,磁感强度为B.导线一端B点固定,A端在沿BA方向的恒力F作用下向右缓慢移动,从而使圆圈缓慢缩小.设在圆圈缩小过程中始终保持圆的形状,导体回路是柔软的,在此过程中F所作功全部变为 (2013?普陀区一模)如图所示是教材规定的探究电源电动势和外电压、内电压关系的专用仪器.
(2013?普陀区一模)如图所示是教材规定的探究电源电动势和外电压、内电压关系的专用仪器. (2013?普陀区一模)如图所示,竖直平面内的3/4圆弧形光滑轨道半径R=1m,A端与圆心O等高,AD为水平面,B点为光滑轨道的最高点且在O的正上方.一小球在A点正上方由静止释放,自由下落至A点进入圆轨道并恰好能通过B点(从A点进入圆轨道时无机械能损失),最后落到水平面C点处.求:
(2013?普陀区一模)如图所示,竖直平面内的3/4圆弧形光滑轨道半径R=1m,A端与圆心O等高,AD为水平面,B点为光滑轨道的最高点且在O的正上方.一小球在A点正上方由静止释放,自由下落至A点进入圆轨道并恰好能通过B点(从A点进入圆轨道时无机械能损失),最后落到水平面C点处.求: