题目内容
 (2013?普陀区一模)如图所示,竖直平面内的3/4圆弧形光滑轨道半径R=1m,A端与圆心O等高,AD为水平面,B点为光滑轨道的最高点且在O的正上方.一小球在A点正上方由静止释放,自由下落至A点进入圆轨道并恰好能通过B点(从A点进入圆轨道时无机械能损失),最后落到水平面C点处.求:
(2013?普陀区一模)如图所示,竖直平面内的3/4圆弧形光滑轨道半径R=1m,A端与圆心O等高,AD为水平面,B点为光滑轨道的最高点且在O的正上方.一小球在A点正上方由静止释放,自由下落至A点进入圆轨道并恰好能通过B点(从A点进入圆轨道时无机械能损失),最后落到水平面C点处.求:(1)小球通过轨道B点的速度大小.
(2)释放点距A点的竖直高度.
(3)落点C到A点的水平距离.
分析:小球恰能通过最高点B时,对轨道的压力为0,重力提供向心力,mg=m
求出B点的速度,从释放点到B点运用动能定理,根据动能定理求出释放点距离A点的高度.
小球离开B点做平抛运动,高度决定时间,根据时间和B点的速度求出水平距离.
| vB2 |
| R |
小球离开B点做平抛运动,高度决定时间,根据时间和B点的速度求出水平距离.
解答:解:(1)小球恰能通过最高点B时有:
mg=m
①
解得:vB=
=
m/s=
m/s
(2)设释放点到A高度h,则有 mg(h-R)=
m
②
联立①②解得:h=1.5R=1.5×1m=1.5m
(3)小球由C到D做平抛运动 R=
gt2③
水平位移xOC=vBt④
联立①③④解得:xOC=
R
所以落点C与A点的水平距离为:
xAC=(
-1)R=(
-1)×1m=0.41m
答:(1)小球通过轨道B点的速度大小为
m/s.
(2)释放点距A点的竖直高度为1.5m.
(3)落点C到A点的水平距离为0.41m.
mg=m
| ||
| R |
解得:vB=
| gR |
| 10×1 |
| 10 |
(2)设释放点到A高度h,则有 mg(h-R)=
| 1 |
| 2 |
| v | 2 B |
联立①②解得:h=1.5R=1.5×1m=1.5m
(3)小球由C到D做平抛运动 R=
| 1 |
| 2 |
水平位移xOC=vBt④
联立①③④解得:xOC=
| 2 |
所以落点C与A点的水平距离为:
xAC=(
| 2 |
| 2 |
答:(1)小球通过轨道B点的速度大小为
| 10 |
(2)释放点距A点的竖直高度为1.5m.
(3)落点C到A点的水平距离为0.41m.
点评:解决本题的关键知道球到达C点时对轨道的压力为0,有mg=m
,以及能够熟练运用动能定理.
| vB2 |
| R |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
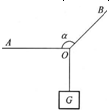 (2013?普陀区一模)如图所示,物体G用两根绳子悬挂,开始时绳OA水平,现将两绳同时沿顺时针方向转过90°,且保持两绳之间的夹角α不变(α>90°),物体保持静止状态.在旋转过程中,设绳OA的拉力为T1,绳OB的拉力为T2,则( )
(2013?普陀区一模)如图所示,物体G用两根绳子悬挂,开始时绳OA水平,现将两绳同时沿顺时针方向转过90°,且保持两绳之间的夹角α不变(α>90°),物体保持静止状态.在旋转过程中,设绳OA的拉力为T1,绳OB的拉力为T2,则( )
 (2013?普陀区一模)如图所示,AB是一根裸导线,单位长度的电阻为R0,一部分弯曲成半径为r0的圆圈,圆圈导线相交处导电接触良好.圆圈所在区域有与圆圈平面垂直的均匀磁场,磁感强度为B.导线一端B点固定,A端在沿BA方向的恒力F作用下向右缓慢移动,从而使圆圈缓慢缩小.设在圆圈缩小过程中始终保持圆的形状,导体回路是柔软的,在此过程中F所作功全部变为
(2013?普陀区一模)如图所示,AB是一根裸导线,单位长度的电阻为R0,一部分弯曲成半径为r0的圆圈,圆圈导线相交处导电接触良好.圆圈所在区域有与圆圈平面垂直的均匀磁场,磁感强度为B.导线一端B点固定,A端在沿BA方向的恒力F作用下向右缓慢移动,从而使圆圈缓慢缩小.设在圆圈缩小过程中始终保持圆的形状,导体回路是柔软的,在此过程中F所作功全部变为 (2013?普陀区一模)如图所示是教材规定的探究电源电动势和外电压、内电压关系的专用仪器.
(2013?普陀区一模)如图所示是教材规定的探究电源电动势和外电压、内电压关系的专用仪器.