题目内容
6.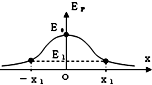 空间某区域存在一电场,一带负电的粒子仅在电场力作用下从x1处沿x轴负方向运动.粒子质量为m,初速度大小为v0,其电势能Ep随坐标x变化的关系如图所示,图线关于纵轴左右对称,以无穷远处为零电势能点,粒子在原点0处电势能为E0,在x1处电势能为E1,则下列说法中正确的是( )
空间某区域存在一电场,一带负电的粒子仅在电场力作用下从x1处沿x轴负方向运动.粒子质量为m,初速度大小为v0,其电势能Ep随坐标x变化的关系如图所示,图线关于纵轴左右对称,以无穷远处为零电势能点,粒子在原点0处电势能为E0,在x1处电势能为E1,则下列说法中正确的是( )| A. | 坐标原点0处两侧电场方向相同 | |
| B. | 由x1运动到0过程电场力做负功 | |
| C. | 粒子经过x1、-x1处速度不相同 | |
| D. | 若粒子能够沿x轴负方向运动越过0点,一定有v0>$\sqrt{\frac{2({E}_{0}-{E}_{1})}{m}}$ |
分析 根据电势能与电势的关系:Ep=qφ,结合分析图象斜率与场强的关系,即可求得原点O处的电场强度;速度根据能量守恒判断;根据斜率读出场强的变化,由F=qE,分析电场力的变化,据动能定理分析速度和过O点速度情况.
解答 解:A、根据电势能与电势的关系:Ep=qφ,场强与电势的关系:E=$\frac{△φ}{△x}$,得:E=$\frac{1}{q}•\frac{△{E}_{p}}{△x}$.Ep-x图象切线的斜率等于$\frac{△{E}_{p}}{△x}$,根据数学知识可知,坐标原点O处切线斜率为零,则坐标原点O两侧的场强大小对称,方向相反,故A错误.
B、据功能关系可知,由x1运动到O过程,电势能增大,电场力做负功,故B正确;
C、由图看出,x1、-x1两处的电势能相等,根据能量守恒定律得知,粒子经过x1、-x1处速度相同,故C错误.
D、根据公式Ep=qφ,可知,该粒子带负电,从x1处到-x1处,电势先降低后升高,电场方向先沿x轴负方向后沿x轴正方向,电场力先沿x轴正方向后沿x轴负方向,粒子只要能通过原点O,就能一直沿x轴运动,设粒子恰好能到达原点O时的速度为v,则根据能量守恒定律得$\frac{1}{2}m{v}^{2}$=E0-E1,v=$\sqrt{\frac{2({E}_{0}-{E}_{1})}{m}}$,当v0>v时,即v0>$\sqrt{\frac{2({E}_{0}-{E}_{1})}{m}}$粒子能够一直沿x轴负方向运动,故D正确.
故选:BD.
点评 解决本题的关键要分析图象斜率的物理意义,判断电势和场强的变化,再根据力学基本规律:牛顿第二定律和能量守恒定律进行分析.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14. 如图所示,两个内壁均光滑,半径不同的半圆轨道固定于地面,一个小球先后从与球心在同一高度的A、B两点由静止开始下滑,通过轨道最低点时( )
如图所示,两个内壁均光滑,半径不同的半圆轨道固定于地面,一个小球先后从与球心在同一高度的A、B两点由静止开始下滑,通过轨道最低点时( )
 如图所示,两个内壁均光滑,半径不同的半圆轨道固定于地面,一个小球先后从与球心在同一高度的A、B两点由静止开始下滑,通过轨道最低点时( )
如图所示,两个内壁均光滑,半径不同的半圆轨道固定于地面,一个小球先后从与球心在同一高度的A、B两点由静止开始下滑,通过轨道最低点时( )| A. | 小球的线速度相等 | B. | 小球的线速度不同 | ||
| C. | 小球对两轨道的压力相同 | D. | 小球对两轨道的压力不同 |
17. 如图所示为氢原子的能级示意图,一群氢原子处于n=3的激发态,在向较低能级跃迁的过程中,用这些光照射逸出功为2.49eV的金属钠,下列说法正确的是( )
如图所示为氢原子的能级示意图,一群氢原子处于n=3的激发态,在向较低能级跃迁的过程中,用这些光照射逸出功为2.49eV的金属钠,下列说法正确的是( )
 如图所示为氢原子的能级示意图,一群氢原子处于n=3的激发态,在向较低能级跃迁的过程中,用这些光照射逸出功为2.49eV的金属钠,下列说法正确的是( )
如图所示为氢原子的能级示意图,一群氢原子处于n=3的激发态,在向较低能级跃迁的过程中,用这些光照射逸出功为2.49eV的金属钠,下列说法正确的是( )| A. | 金属钠表面逸出光电子的初动能的最大值为9.60eV | |
| B. | 这群氢原子能发出2种不同频率的光,且均能使金属钠发生光电效应 | |
| C. | 从n=3的激发态跃迁到n=2的激发态时所发出的光的波长最短 | |
| D. | 用动能为2.0eV的电子轰击处于n=3的激发态的氢原子,可以使它们跃迁到n=4的激发态 |
1. 如图所示,沿波的传播方向上有间距均为1m的a、b、c、d、e、f六个质点,它们均静止在各自的平衡位置.一列振幅为10cm的简谐横波以2m/s的速度水平向右传播.t=0时刻,质点a开始振动,其运动方向向上,t=1.5s时刻,质点a第一次到达最低点,则下列判断正确的是( )
如图所示,沿波的传播方向上有间距均为1m的a、b、c、d、e、f六个质点,它们均静止在各自的平衡位置.一列振幅为10cm的简谐横波以2m/s的速度水平向右传播.t=0时刻,质点a开始振动,其运动方向向上,t=1.5s时刻,质点a第一次到达最低点,则下列判断正确的是( )
 如图所示,沿波的传播方向上有间距均为1m的a、b、c、d、e、f六个质点,它们均静止在各自的平衡位置.一列振幅为10cm的简谐横波以2m/s的速度水平向右传播.t=0时刻,质点a开始振动,其运动方向向上,t=1.5s时刻,质点a第一次到达最低点,则下列判断正确的是( )
如图所示,沿波的传播方向上有间距均为1m的a、b、c、d、e、f六个质点,它们均静止在各自的平衡位置.一列振幅为10cm的简谐横波以2m/s的速度水平向右传播.t=0时刻,质点a开始振动,其运动方向向上,t=1.5s时刻,质点a第一次到达最低点,则下列判断正确的是( )| A. | 各质点开始振动后的频率均为2Hz | |
| B. | t=2s时刻,质点c、e的速度均为最大值 | |
| C. | t=3s时刻,波恰好传播到质点f | |
| D. | 在2s<t<3s这段时间内,质点b、d的速度先增大后减小 | |
| E. | a点的振动表达式为x=10sin(πt)cm |
11. 如图甲所示,质量为4kg的物体在水平推力作用下开始运动,推力大小F随位移大小x变化的情况如图乙所示,物体与地面间的动摩擦因数为μ=0.5,g取10m/s2,则( )
如图甲所示,质量为4kg的物体在水平推力作用下开始运动,推力大小F随位移大小x变化的情况如图乙所示,物体与地面间的动摩擦因数为μ=0.5,g取10m/s2,则( )
 如图甲所示,质量为4kg的物体在水平推力作用下开始运动,推力大小F随位移大小x变化的情况如图乙所示,物体与地面间的动摩擦因数为μ=0.5,g取10m/s2,则( )
如图甲所示,质量为4kg的物体在水平推力作用下开始运动,推力大小F随位移大小x变化的情况如图乙所示,物体与地面间的动摩擦因数为μ=0.5,g取10m/s2,则( )| A. | 物体先做加速运动,推力撤去才开始做减速运动 | |
| B. | 物体在水平面上运动的最大位移是10m | |
| C. | 物体运动的最大速度为20m/s | |
| D. | 物体在运动中的加速度先变小后不变 |
18.下列说法正确的是( )
| A. | 方程式${\;}_{92}^{238}$U→${\;}_{90}^{234}$Th+${\;}_{2}^{4}$He是核裂变反应方程 | |
| B. | 方程式${\;}_{1}^{1}$H+${\;}_{1}^{2}$H→${\;}_{2}^{3}$He+γ是核聚变反应方程 | |
| C. | 氢原子光谱是连续的 | |
| D. | 氢原子从某激发态跃迁至基态要放出特定频率的光子 |
16.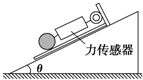 一足够长的倾角为θ的斜面固定在水平面上,在斜面顶端放置一长木板,木板与斜面之间的动摩擦因数为μ,木板上固定一力传感器,连接传感器和光滑小球间是一平行于斜面的轻杆,如图所示,现由静止释放木板,木板沿斜面下滑,稳定时传感器的示数为F1,当木板固定时,传感器的示数为F2.则下列说法正确的是( )
一足够长的倾角为θ的斜面固定在水平面上,在斜面顶端放置一长木板,木板与斜面之间的动摩擦因数为μ,木板上固定一力传感器,连接传感器和光滑小球间是一平行于斜面的轻杆,如图所示,现由静止释放木板,木板沿斜面下滑,稳定时传感器的示数为F1,当木板固定时,传感器的示数为F2.则下列说法正确的是( )
 一足够长的倾角为θ的斜面固定在水平面上,在斜面顶端放置一长木板,木板与斜面之间的动摩擦因数为μ,木板上固定一力传感器,连接传感器和光滑小球间是一平行于斜面的轻杆,如图所示,现由静止释放木板,木板沿斜面下滑,稳定时传感器的示数为F1,当木板固定时,传感器的示数为F2.则下列说法正确的是( )
一足够长的倾角为θ的斜面固定在水平面上,在斜面顶端放置一长木板,木板与斜面之间的动摩擦因数为μ,木板上固定一力传感器,连接传感器和光滑小球间是一平行于斜面的轻杆,如图所示,现由静止释放木板,木板沿斜面下滑,稳定时传感器的示数为F1,当木板固定时,传感器的示数为F2.则下列说法正确的是( )| A. | 稳定后传感器的示数一定为零 | B. | tan θ=$\frac{μ{F}_{1}}{{F}_{2}}$ | ||
| C. | cot θ=$\frac{{F}_{1}}{μ{F}_{2}}$ | D. | cot θ=$\frac{{F}_{2}}{μ{F}_{1}}$ |