题目内容
7.如图甲所示,由斜面AB和水平面BC组成的物块,放在光滑水平地面上,斜面AB部分光滑、AB长度为s=2.5m,水平部分BC粗糙.物块左侧与竖直墙壁之间连接着一个力传感器,当传感器受压时示数为正值,被拉时为负值.上表面与BC等高且粗糙程度相同的木板DE紧靠在物块的右端,木板DE质量M=4kg,长度L=1.5m.一可视为质点的滑块从A点由静止开始下滑,经B点由斜面转到水平面时速度大小不变.滑块从A到C过程中,传感器记录到力和时间的关系如图乙所示.g取10m/s2,求: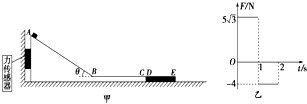
(1)斜面AB的倾角θ;
(2)滑块的质量m;
(3)滑块到达木板DE右端时的速度大小.
分析 (1)由图象可知,物块在AB面上运动时,压力传感器为正值,在BC面上运动时,压力传感器为负值,根据图象得出在斜面上运动的时间,根据牛顿第二定律,结合位移时间公式求出斜面AB的倾角.
(2)在0-1s内对斜面体ABC受力分析,抓住压力传感器的示数,结合共点力平衡求出木块的质量.
(3)根据速度时间公式求出物块到达B点的速度,结合图线得出在BC上滑动时所受的摩擦力,根据牛顿第二定律求出匀减速运动的加速度大小,从而得出动摩擦因数的大小,滑上DE段后,对木块和木板分析,根据牛顿第二定律和运动学公式,抓住位移之差等于DE的长度求出运动的时间以及滑块到达木板DE右端时的速度.
解答 (1)在0~1 s内木块沿斜面匀加速下滑:
mgsin θ=ma①
s=$\frac{1}{2}$at2②
由图知:t=1 s
解得:sin θ=$\frac{1}{2}$
θ=30°.③
(2)在0~1 s内对斜面体ABC受力分析:
mgcos θ sin θ-F=0④
由图知:F=5$\sqrt{3}$ N
解得:m=2 kg.⑤
(3)木块到达B点的速度:
vB=at=gsin θt=5 m/s⑥
1~2 s木块在BC部分做减速运动:
μmg=ma′⑦
对斜面体,由图象知:
μmg=F=4 N⑧
解得:a′=2 m/s2,μ=0.2
木块到达C点时:
vC=vB-a′t=vB-μgt=3 m/s⑨
木块滑上木板DE时:
对木块:-μmg=ma1⑩
对木板:μmg=Ma2⑪
解得:a1=-2 m/s2,a2=1 m/s2
设木块在木板上的滑行时间为t,
x木块=vCt+$\frac{1}{2}$a1t2
x木板=$\frac{1}{2}$a2t2
L=x木块-x木板
解得:t=1 s⑫
此时,木块速度:v木块=vC-a1t=1 m/s⑬
木板速度:v木板=a2t=1 m/s
所以木块恰好滑到木板右端,速度为1 m/s.
答:(1)斜面AB的倾角θ为30°;
(2)滑块的质量m为2kg;
(3)滑块到达木板DE右端时的速度大小为1m/s.
点评 本题考查了动力学知识与图象的综合,理清木块在整个过程中的运动规律,结合牛顿第二定律和运动学公式进行求解,难度中等.

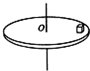 一圆盘可绕通过其中心且垂直于盘面的竖直轴转动,现在圆盘上放置一个木块,当圆盘匀速转动时,木块随圆盘一起运动,如图所示,那么下列说法正确的是( )
一圆盘可绕通过其中心且垂直于盘面的竖直轴转动,现在圆盘上放置一个木块,当圆盘匀速转动时,木块随圆盘一起运动,如图所示,那么下列说法正确的是( )| A. | 木块受到重力、支持力、摩擦力、向心力的作用 | |
| B. | 木块受到重力、支持力、摩擦力的作用 | |
| C. | 木块受到的摩擦力,方向始终是指向圆盘中心 | |
| D. | 木块受到的摩擦力,方向与木块的运动速度方向相反 |
| A. | 小球的机械能减少了$\frac{mgH}{3}$ | B. | 小球的动能增加了$\frac{mgH}{3}$ | ||
| C. | 小球的电势能增加了$\frac{mgH}{3}$ | D. | 小球的重力势能减少了mgH |
| A. | 吸热时其内能可以不变 | B. | 吸热时其内能一定不变 | ||
| C. | 不吸热也不放热时其内能可以减小 | D. | 不吸热也不放热时其内能一定不变 |
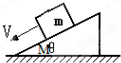 如图所示,放置在水平地面上的直角劈M上有一个质量为m的物体,在其上匀速下滑,M保持静止.若对正在下滑的m加一水平向右的推力,且该推力逐渐加大,在m继续下滑的过程中,直角劈M一直保持静止.正确的说法是( )
如图所示,放置在水平地面上的直角劈M上有一个质量为m的物体,在其上匀速下滑,M保持静止.若对正在下滑的m加一水平向右的推力,且该推力逐渐加大,在m继续下滑的过程中,直角劈M一直保持静止.正确的说法是( )| A. | M对地面的压力等于(M+m)g | B. | M对地面的压力大于(M+m)g | ||
| C. | 地面对M没有摩擦力 | D. | 地面对M有向左的摩擦力 |
| A. | 导体两端的电压不为零,导体内部的场强为零 | |
| B. | 导体两端的电压不为零,导体内部的场强不为零 | |
| C. | 导体两端的电压为零,导体内部的场强不为零 | |
| D. | 导体两端的电压为零,导体内部的场强为零 |
 如图所示,把质量为0.5kg的石块从30m高处的A点以300角斜向上方抛出,初速度是v0=5m/s(不计空气阻力,取g=10m/s2)求:
如图所示,把质量为0.5kg的石块从30m高处的A点以300角斜向上方抛出,初速度是v0=5m/s(不计空气阻力,取g=10m/s2)求: 如图所示,有一半圆形玻璃砖,折射率为$\sqrt{2}$,AB为直径,O为圆心.一束宽度恰等于玻璃砖半径的单色平行光垂直于AB从空气射入玻璃砖,其中心光线通过O点.则光束中的光线射出玻璃砖时最大的折射角为45°,并且在图中画出中间一条光线在玻璃砖内和玻璃砖后的光路.
如图所示,有一半圆形玻璃砖,折射率为$\sqrt{2}$,AB为直径,O为圆心.一束宽度恰等于玻璃砖半径的单色平行光垂直于AB从空气射入玻璃砖,其中心光线通过O点.则光束中的光线射出玻璃砖时最大的折射角为45°,并且在图中画出中间一条光线在玻璃砖内和玻璃砖后的光路. 如图所示正方形线框abcd边长L=0.1m,每边电阻1Ω,在磁感应强度B=0.3T的匀强磁场中绕cd以每分钟$\frac{2400\sqrt{2}}{π}$转的转速匀速转动,cd两点与外电路相连,外电路电阻R=1Ω,求
如图所示正方形线框abcd边长L=0.1m,每边电阻1Ω,在磁感应强度B=0.3T的匀强磁场中绕cd以每分钟$\frac{2400\sqrt{2}}{π}$转的转速匀速转动,cd两点与外电路相连,外电路电阻R=1Ω,求