题目内容
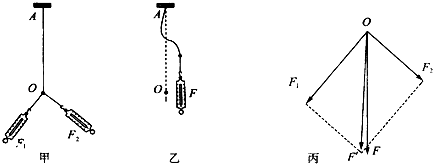
【题目】一轻质弹簧原长为L,劲度系数k等于200N/m,将其上端固定在天花板上的O点,如图1所示.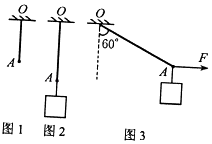
(1)在其下端点A处悬挂重为32N的物块,静止后如图2所示,求弹簧的伸长量△x1 .
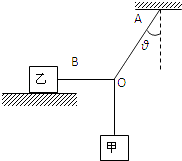
(2)在图2中A点用一水平外力向右缓慢拉动,使橡皮筋与竖直方向成60°角时保持静止,如图3所示,求弹簧的伸长量△x2和此时拉力F的大小.
【答案】
(1)
解:根据胡可定律得k△x1=mg,
可得: ![]() =
= ![]() =0.16m
=0.16m
(2)
解:对A点受力分析,作出力的合成图如图所示
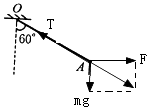
可知弹簧受到的拉力T= ![]() =
= ![]() ,
,
根据胡可定律得:k△x2=T
解得:△x2= ![]() m=0.32m;
m=0.32m;
拉力F=Tsin60°= ![]()
【解析】(1)弹簧受到的拉力大小等于物块的重力,利用胡克定律列式,求出弹簧的伸长量;(2)画出受力分析图,求出弹簧受到的弹力,利用胡克定律列式,求出弹簧的伸长量;根据共点力的平衡条件求解拉力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目