题目内容
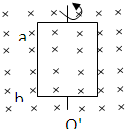 匝数为N、面积为S、总电阻为R的矩形闭合线圈,在磁感应强度为B的匀强磁场中按如图所示方向(俯视逆时针)以角速度ω绕轴OO′匀速转动.t=0时线圈平面与磁感应线垂直,规定adcba的方向为电流的正方向,求:
匝数为N、面积为S、总电阻为R的矩形闭合线圈,在磁感应强度为B的匀强磁场中按如图所示方向(俯视逆时针)以角速度ω绕轴OO′匀速转动.t=0时线圈平面与磁感应线垂直,规定adcba的方向为电流的正方向,求:(1)线圈转动过程中感应电动势瞬时值的表达式.
(2)线圈转到与图示位置成60°角时的瞬时电流.
(3)线圈转动一周过程中外力做的功.
分析:(1)先求出线圈中产生的感应电动势的最大值表达式为Em=NBSω,再由从中性面开始计时,从而确定感应电动势瞬时值的表达式.
(2)由感应电动势的瞬时表达式,结合闭合电路欧姆定律可得,线圈转到与图示位置成60°角时的瞬时电流的大小;
(3)线圈转动一周的过程中外力做的功,完全给电阻用来发热,因此由有效值来计算在一周发热量.
(2)由感应电动势的瞬时表达式,结合闭合电路欧姆定律可得,线圈转到与图示位置成60°角时的瞬时电流的大小;
(3)线圈转动一周的过程中外力做的功,完全给电阻用来发热,因此由有效值来计算在一周发热量.
解答:解:(1)线圈产生的感应电动势的最大值为Em=NBSω,
则线圈转动过程中感应电动势的瞬时值为e=NBSωsinωt
(2)线圈转到与图示位置成60°角时的瞬时电流
i=
=
sin60°=
(3)感应电动势的有效值为:
E=
=
根据能量守恒定律,线圈转动一周过程中外力做的功:
W=
T=
答:(1)线圈转动过程中感应电动势瞬时值的表达式e=NBSωsinωt.
(2)线圈转到与图示位置成60°角时的瞬时电流的大小为
.
(3)线圈转动一周的过程中外力做的功为
.
则线圈转动过程中感应电动势的瞬时值为e=NBSωsinωt
(2)线圈转到与图示位置成60°角时的瞬时电流
i=
| e |
| R |
| NBSω |
| R |
| ||
| 2R |
(3)感应电动势的有效值为:
E=
| Em | ||
|
| NBSω | ||
|
根据能量守恒定律,线圈转动一周过程中外力做的功:
W=
| E2 |
| R |
| πN2B2S2ω |
| R |
答:(1)线圈转动过程中感应电动势瞬时值的表达式e=NBSωsinωt.
(2)线圈转到与图示位置成60°角时的瞬时电流的大小为
| ||
| 2R |
(3)线圈转动一周的过程中外力做的功为
| πN2B2S2ω |
| R |
点评:从中性面开始计时,则瞬时表达就是正弦,若是垂直中性面计时,则瞬时表达式就是余弦;由法拉第电磁感应定律可得平均感应电动势,而E=BLV可得瞬时感应电动势;求电阻发热,则必须将交流电的有效值代入计算.

练习册系列答案
相关题目
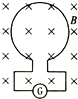 在物理实验中,要测定磁场的磁感应强度,可用一个探测线圈与一个冲击电流计(可测定通过电路的电荷量)串联后测量,原理图如图所示,若已测得匀强磁场的磁感应强度为B,又知探测线圈的匝数为n,面积为S,线圈与冲击电流计组成的回路电阻为R,实验开始时线圈平面与磁场垂直,若把探测线圈翻转180°,则此过程中冲击电流计测出的通过线圈的电荷量是( )
在物理实验中,要测定磁场的磁感应强度,可用一个探测线圈与一个冲击电流计(可测定通过电路的电荷量)串联后测量,原理图如图所示,若已测得匀强磁场的磁感应强度为B,又知探测线圈的匝数为n,面积为S,线圈与冲击电流计组成的回路电阻为R,实验开始时线圈平面与磁场垂直,若把探测线圈翻转180°,则此过程中冲击电流计测出的通过线圈的电荷量是( )| A、0 | ||
B、
| ||
C、
| ||
D、
|
 如图所示为一内阻不计,匝数为N,面积为S的矩形线框,在磁感应强度为B的匀强磁场中绕垂直于磁场方向的轴OO’以角速度ω匀速转动,以线?平面与磁场方向平行的位置开始计时,线圈通过滑环和一理想变压器相连,滑片P上下移动可改变输出电压,副线圈接有可调电阻R.下列判断正确的是( )
如图所示为一内阻不计,匝数为N,面积为S的矩形线框,在磁感应强度为B的匀强磁场中绕垂直于磁场方向的轴OO’以角速度ω匀速转动,以线?平面与磁场方向平行的位置开始计时,线圈通过滑环和一理想变压器相连,滑片P上下移动可改变输出电压,副线圈接有可调电阻R.下列判断正确的是( )| A、矩形线圈产生的感应电动势瞬时值表达式是e=NBSωcosωt | ||
B、在0~
| ||
| C、在只增大R的阻值时,电压表的示数也增大 | ||
| D、若只将滑片P向上移动时电流表的示数增大 |
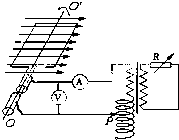
 如图所示,发电机内部线圈处于磁铁和圆柱形铁芯之间的径向磁场中,磁铁的N、S极间的过渡区域宽度很小,可忽略不计.线圈的匝数为N、面积为S,总电阻为r,线圈所在位置的磁感应强度大小为B.当线圈以角速度ω匀速转动时,额定电压为U、电阻为R的小灯泡在电路中恰能正常发光,则( )
如图所示,发电机内部线圈处于磁铁和圆柱形铁芯之间的径向磁场中,磁铁的N、S极间的过渡区域宽度很小,可忽略不计.线圈的匝数为N、面积为S,总电阻为r,线圈所在位置的磁感应强度大小为B.当线圈以角速度ω匀速转动时,额定电压为U、电阻为R的小灯泡在电路中恰能正常发光,则( )| A、感应电动势的最大值是NBSω | ||||
B、感应电动势的有效值是
| ||||
C、感应电动势的有效值是(1+
| ||||
| D、转动过程中线圈中的磁通量始终为零 |

 如图所示,矩形线框绕与匀强磁场垂直的轴OO′按图示的方向以角速度ω匀速转动,线框的匝数为n、面积为S、电阻为r,磁感应强度大小为B,方向水平向右.线框的输出端与两个金属滑环相连,阻值为R的定值电阻、理想的交流电流表处通过电刷和导线与滑环连接.当线框转到与磁场平行时,开始计时,规定从F通过电阻R到E为电流的正方向,下列说法正确的是( )
如图所示,矩形线框绕与匀强磁场垂直的轴OO′按图示的方向以角速度ω匀速转动,线框的匝数为n、面积为S、电阻为r,磁感应强度大小为B,方向水平向右.线框的输出端与两个金属滑环相连,阻值为R的定值电阻、理想的交流电流表处通过电刷和导线与滑环连接.当线框转到与磁场平行时,开始计时,规定从F通过电阻R到E为电流的正方向,下列说法正确的是( )