Question

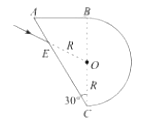
【题目】某透明介质的截面图如图所示，直角三角形的直角边BC与半圆形直径重合，∠ACB = 30°，半圆形的半径为R， —束光线从E点射入介质，其延长线过半圆形的圆心O，且E、O两点距离为R，已知光在真空的传播速度为c，介质折射率为。求：

(1)光线在E点的折射角并画出光路图；

(2)光线进入介质到射到圆弧的距离和时间。

Answer 1

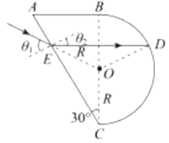【答案】(1)30°；；(2)； 。

【解析】

(1)由题

OE＝OC＝R

则：△OEC为等腰三角形

∠OEC＝∠ACB＝30°

所以入射角：

θ1＝60°

由折射定律：n＝ 可得：

sinθ2=，θ2＝30°

由几何关系：∠OED＝30°，则折射光平行于AB的方向，如图；

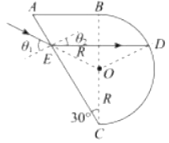
(2)折射光平行于AB的方向，所以：

ED=2Rcos30°=

光在介质内的速度：v＝，传播的时间：

t＝

联立可得：

t＝