��Ŀ����
����Ŀ����ͼ����ʾ���ֲ�б���ˮƽ��ļн�Ϊ30��������Ϊ3kg��С��飨����Ϊ�ʵ㣩�ɾ�ֹ��A����һ��б�����ϵĺ㶨�����������˶�������һ��ʱ���ȥ��������С����ܵ������λ��C��С����ϻ������е�v��tͼ����ͼ����ʾ����A��Ϊ�����ܲο��㣬g=10m/s2��������˵����ȷ���ǣ� ��
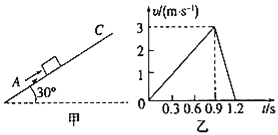
A. С��������������Ϊ54J
B. С������ʱ��ƽ���ٶ������ʱ��ƽ���ٶȴ�С֮��Ϊ3��1
C. С�����б���Ķ�Ħ������Ϊ![]()
D. ����F�Ĵ�СΪ40N
���𰸡�D
���������������������ͼ�����С������������λ�ƣ������ü��ι�ϵ������������߶ȣ�����![]() ���С�������������ܣ�����ͼ�����С������ʱ��ƽ���ٶ������ʱ��ƽ���ٶȴ�С���ɵó��𰸣�����ͼ�����С�������˶��ļ��ٶȴ�С��Ȼ�����ţ�ٵڶ��������С�����б���Ķ�Ħ������������ͼ�����С�������˶��ļ��ٶȴ�С��Ȼ�����ţ�ٵڶ������������F�Ĵ�С��
���С�������������ܣ�����ͼ�����С������ʱ��ƽ���ٶ������ʱ��ƽ���ٶȴ�С���ɵó��𰸣�����ͼ�����С�������˶��ļ��ٶȴ�С��Ȼ�����ţ�ٵڶ��������С�����б���Ķ�Ħ������������ͼ�����С�������˶��ļ��ٶȴ�С��Ȼ�����ţ�ٵڶ������������F�Ĵ�С��
��ͼ���֪���������������λ��Ϊ![]() ���ɼ��ι�ϵ�ã�С������������߶�Ϊ
���ɼ��ι�ϵ�ã�С������������߶�Ϊ![]() ����С��������������Ϊ
����С��������������Ϊ![]() ��A����С������ʱ��ƽ���ٶ������ʱ��ƽ���ٶȴ�СΪ
��A����С������ʱ��ƽ���ٶ������ʱ��ƽ���ٶȴ�СΪ![]() �����С֮��Ϊ1��1��B������ͼ����ʾͼ���֪�������˶��ļ��ٶȴ�СΪ
�����С֮��Ϊ1��1��B������ͼ����ʾͼ���֪�������˶��ļ��ٶȴ�СΪ![]() �����ȼ���ֱ���˶������У���ţ�ٵڶ�����֪
�����ȼ���ֱ���˶������У���ţ�ٵڶ�����֪![]() �����
�����![]() ��C�������˶��ļ��ٶȴ�СΪ��
��C�������˶��ļ��ٶȴ�СΪ�� ![]() ����б�淽�����ţ�ٵڶ����ɿɵ�
����б�淽�����ţ�ٵڶ����ɿɵ�![]() ���������ݿɽ��F=40N����D��ȷ��
���������ݿɽ��F=40N����D��ȷ��