题目内容
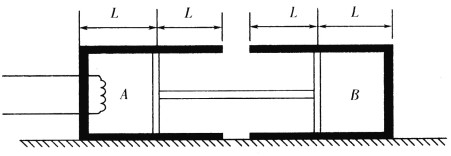
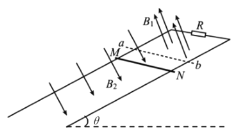
【题目】如图所示,在倾角为θ的斜面内有两条足够长的不计电阻的平行金属导轨,导轨宽度为L,导轨上端连有阻值为R的电阻;在垂直于导轨边界ab上方轨道空间内有垂直于导轨向上的均匀变化的匀强磁场B1。边界ab下方导轨空间内有垂直于导轨向下的匀强磁场B2。电阻也为R、质量为m的导体棒MN垂直于导轨放置,磁场B1随时间均匀减小,且边界ab上方轨道平面内磁通量变化率大小为k,MN静止且受到导轨的摩擦力为零;撤去磁场B2,MN从静止开始在较短的时间t内做匀加速运动通过的距离为x。重力加速度为g。
(1)求磁场B2的磁感应强度大小;
(2)求导体棒MN与导轨之间动摩擦因数;
(3)若再撤去B1,恢复B2,MN从静止开始运动,求其运动过程中的最大动能。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)当磁场B1随时间均匀减小,设回路中感应电动势为E,感应电流为I,则根据法拉第电磁感应定律
![]()
根据闭合电路欧姆定律
![]()
MN静止且受到导轨的摩擦力为零,受力平衡
![]()
解得
![]()
(2)撤去磁场B2,设MN从静止开始做匀加速运动过程中的加速度为a,导体棒MN与导轨之间动摩擦因数为μ,则
![]()
根据牛顿第二定律
![]()
解得
![]()
(3)若再撤去B1,恢复B2,设MN运动过程中的最大速度为vm,最大动能为Ekm,稳定时
![]()
导体切割磁感线
![]()
通过回路的感应电流
![]()
安培力为
![]()
最大动能
![]()
联立方程解得
![]()

练习册系列答案
相关题目