题目内容
（2008?海南）一探月卫星在地月转移轨道上运行，某一时刻正好处于地心和月心的连线上，卫星在此处所受地球引力与月球引力之比为4：1．已知地球与月球的质量之比约为81：1，则该处到地心与到月心的距离之比约为
9：2
9：2
．分析：根据万有引力定律表示出地球对卫星的引力和月球对卫星的引力．
根据引力之比为4：1求出卫星距地心距离与距月心距离之比．
根据引力之比为4：1求出卫星距地心距离与距月心距离之比．
解答：解：设月球质量为M，地球质量就为81M．
卫星距地心距离为r1，卫星距月心距离为r2 ．
由于地球对它的引力和月球对它的引力相等，根据万有引力定律得：
=4×
=
则该处到地心与到月心的距离之比约为9：2．
故答案为：9：2
卫星距地心距离为r1，卫星距月心距离为r2 ．
由于地球对它的引力和月球对它的引力相等，根据万有引力定律得：
| G?81Mm | ||
|
| GMm | ||
|
| r1 |
| r2 |
| 9 |
| 2 |
则该处到地心与到月心的距离之比约为9：2．
故答案为：9：2
点评：该题考查的是万有引力定律的应用，要能够根据题意列出等式，去解决问题．
练习册系列答案
名校课堂系列答案
相关题目
（2008?海南）某实验室中悬挂着一弹簧振子和一单摆，弹簧振子的弹簧和小球（球中间有孔）都套在固定的光滑竖直杆上．某次有感地震中观察到静止的振子开始振动4.0s后，单摆才开始摆动．此次地震中同一震源产生的地震纵波和横波的波长分别为10km和5.0km，频率为1.0Hz．假设该实验室恰好位于震源的正上方，求震源离实验室的距离．
（2008?海南）如图，质量为M的楔形物块静置在水平地面上，其斜面的倾角为θ．斜面上有一质量为m的小物块，小物块与斜面之间存在摩擦．用恒力F沿斜面向上拉小物块，使之匀速上滑．在小物块运动的过程中，楔形物块始终保持静止．地面对楔形物块的支持力为（ ）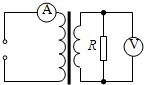
（2008?海南）如图，理想变压器原副线圈匝数之比为4：1．原线圈接入一电压为u=U0sinωt的交流电源，副线圈接一个R=27.5Ω的负载电阻．若U0=220