题目内容
某人造卫星距地h,地球半径为R,质量为M,地面重力加速度为g,万有引力恒量为G.
(1)试分别用h、R、M、G表示卫星的周期T、线速度V、角速度ω.
(2)试分别用h、R、g表示卫星周期T、线速度V、角速度ω.
(1)试分别用h、R、M、G表示卫星的周期T、线速度V、角速度ω.
(2)试分别用h、R、g表示卫星周期T、线速度V、角速度ω.
分析:(1)由万有引力提供向心力列出等式求解
(2)根据万有引力等于重力运用黄金代换式GM=gR2求解.
(2)根据万有引力等于重力运用黄金代换式GM=gR2求解.
解答:解:(1)由万有引力提供向心力,有
=m
T=
=m
v=
=mω2(R+h)
ω=
(2)根据地面附近的万有引力近似等于重力,
则
=mg
GM=gR2,
所以T=
,v=
,ω=
答:(1)用h、R、M、G表示,T=
,v=
,ω=
.
(2)用h、R、g表示,T=
,v=
,ω=
.
| GMm |
| (R+h)2 |
| 4π2(R+h) |
| T2 |
T=
|
| GMm |
| (R+h)2 |
| v2 |
| R+h |
v=
|
| GMm |
| (R+h)2 |
ω=
|
(2)根据地面附近的万有引力近似等于重力,
则
| GMm |
| R2 |
GM=gR2,
所以T=
|
|
|
答:(1)用h、R、M、G表示,T=
|
|
|
(2)用h、R、g表示,T=
|
|
|
点评:本题主要考查了圆周运动向心力公式和万有引力定律的直接应用,运用黄金代换式GM=gR2求出问题是考试中常见的方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
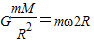 对人造卫星有:
对人造卫星有: