��Ŀ����
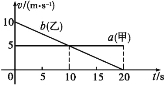
����Ŀ����ͼ��ʾ��������ΪM��С���й�һ���ڣ���������Ϊm0 �� С�����Ͱڣ�һ���Ժ㶨�ٶ�v�ع⻬ˮƽ�����˶�����λ�������������Ϊm�ľ�ֹľ�鷢����ײ������ײʱ�伫�̣�������ײ�����У�����������ܷ������У� ��
A.����ľ�顢������ٶȾ����ܱ仯����仯����ٶȷֱ�Ϊv1��v2��v3 �� ���������㣨M+m��v=Mv1+mv2+m0v3
B.������ٶȲ��䣬����ľ����ٶȱ�Ϊv1��v2 �� ������Mv=Mv1+mv2
C.������ٶȲ��䣬����ľ����ٶȾ���Ϊv1 �� ������Mv=��M+m��v1
D.���Ͱ�����ٶȾ���Ϊv1 �� ľ����ٶȱ�Ϊv2 �� �����㣨M+m0��v=��M+m0��v1
���𰸡�B,C
���������⣺��ײ��˲��С����ľ����ɵ�ϵͳ�����غ㣬������ٶ���˲�䲻�䣬����ij��ٶȷ���Ϊ������������С����ľ����ٶȱ�v1��v2 �� �ɶ����غ㶨�ɵã�
MV=MV1+mV2��
������С����ľ���ٶ���ͬ���ɶ����غ㶨�ɵã�
MV=��M+m��V�䣮
��BC��ȷ��AD����
��ѡ��BC��
�����㾫����������Ĺؼ���������ܹ�ϵ�����֪ʶ�����յ�ֻ���������ɵ���������ʱ������Ļ�е���غ㣻�������������Ĺ����������������ܵļ���:W G =E p1 -E p2�������������������Ĺ��������嶯�ܵı仯:W �� =E k2 -E k1 �����ܶ������������������ɵ�����֮����������������Ĺ����������е�ܵı仯:W F =E 2 -E 1���Լ��Զ����غ㶨�ɵ����⣬�˽���غ㶨�ɳ�����������ϵͳ����������ϵͳ���������ĺ���Ϊ�㣻ϵͳ���ܵ������ĺ����䲻Ϊ�㣬��ϵͳ����������С�öࣻϵͳ���������ĺ����䲻Ϊ�㣬����ij�������ϵķ���Ϊ�㣬���ڸ÷�����ϵͳ���ܶ����ķ������ֲ��䣮

 �ŵ������ϵ�д�
�ŵ������ϵ�д� 53������ϵ�д�
53������ϵ�д�