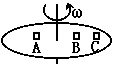题目内容
如图所示，可视为质点的、质量为m的小球，在半径为R的竖直放置的光滑圆形管道内做圆周运动，下列有关说法中正确的是（ ）
| A．小球能够通过最高点时的最小速度为0 |
B．小球能够通过最高点时的最小速度为 |
| C．如果小球在最高点时的速度大小为2，则此时小球对管道的外壁有作用力 |
D．如果小球在最低点时的速度大小为 ，则小球通过最高点时与管道间无相互作用力 |
ACD
解析试题分析: 在最高点，由于外管或内管都可以对小球产生弹力作用，当小球的速度等于0时，内管对小球产生弹力，大小为mg，故最小速度为0．故A正确，B错误；设管道对小球的弹力大小为F，方向竖直向下．由牛顿第二定律得：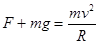
，代入解得F=3mg＞0，方向竖直向下．根据牛顿第三定律得知：小球对管道的弹力方向竖直向上，即小球对管道的外壁有作用力．故C正确；设最低点的速度为v1，最高点的速度为v2，由机械能守恒定律，
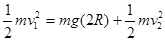，如果小球在最低点时的速度大小为，最高点的速度，最高点向心力，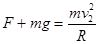
，得F=0；则小球通过最高点时与管道间无相互作用力，故D正确。
考点：向心力公式
练习册系列答案
综合自测系列答案
相关题目
一个电子钟的秒针角速度为 ( )
| A．πrad/s | B．2πrad/s |
| C．π/30 rad/s | D．π/60 rad/s |
长度为1m的轻杆OA，A端有一质量为2kg的小球，以O点为圆心，在竖直平面内做圆周运动，如图所示，小球通过最高点时的速度为3m/s，取g=10m/s2，则此时小球将（ ）
| A．受到18N的拉力 | B．受到38N的支持力 | C．受到2N的拉力 | D．受到2N的支持力 |
一轻杆一端固定质量为m的小球，以另一端O为圆心，使小球在竖直面内做半径为R的圆周运动，如图所示，则下列说法正确的是 （ ）
| A．小球过最高点时，杆所受到的弹力可以等于零 |
B．小球过最高点的最小速度是 |
| C．小球过最高点时，杆对球的作用力一定随速度增大而增大 |
| D．小球过最高点时，杆对球的作用力一定随速度增大而减小 |
物体在做匀速圆周运动的过程中，保持不变的物理量为（ ）
| A．线速度 | B．角速度 | C．向心力 | D．向心加速度 |
如图所示，轻杆长为L.一端固定在水平轴上的O点，另一端系一个小球(可视为质点)．小球以O为圆心在竖直平面内做圆周运动，且能通过最高点，g为重力加速度．下列说法正确的是 
A．小球通过最高点时速度不可能小于 |
| B．小球通过最高点时所受轻杆的作用力可能为零 |
| C．小球通过最高点时所受轻杆的作用力随小球速度的增大而增大 |
| D．小球通过最高点时所受轻杆的作用力随小球速度的增大而减小 |