题目内容
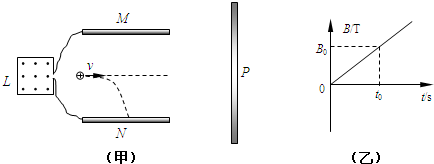
如图(甲)所示,一竖直放置的边长为L的正方形导线框,其内有垂直框面向外的均匀变化的磁场,磁场变化如图(乙)所示.导线框两端分别连平行板电容器的两极板M、N,M、N的长度和它们之间的距离都是d,两平行板所在平面与纸面垂直.
(1)一质子沿M、N两板正中央水平射入,恰好打在N板的中点处.已知质子的质量和电量分别为m、e,求M、N两板间的电压UMN和质子入射的初速度v0.
(2)若在M、N间加一垂直纸面的匀强磁场B,质子以初速度v沿两极板的正中央入射时,恰好沿直线通过两板,求M、N间所加磁场B的大小和方向.
(3)若在M、N的右侧有一垂直M、N板的长接收板P,且在接收板与M、N间也存在(2)中所加的同样大小与方向的磁场B,则质子以直线通过M、N板之后恰好没有碰到P板.求M板右端到P板的距离.
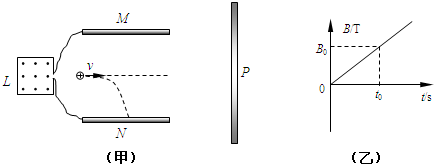
(1)一质子沿M、N两板正中央水平射入,恰好打在N板的中点处.已知质子的质量和电量分别为m、e,求M、N两板间的电压UMN和质子入射的初速度v0.
(2)若在M、N间加一垂直纸面的匀强磁场B,质子以初速度v沿两极板的正中央入射时,恰好沿直线通过两板,求M、N间所加磁场B的大小和方向.
(3)若在M、N的右侧有一垂直M、N板的长接收板P,且在接收板与M、N间也存在(2)中所加的同样大小与方向的磁场B,则质子以直线通过M、N板之后恰好没有碰到P板.求M板右端到P板的距离.

(1)设平行板电容器两端的电压是U,
则由法拉第电磁感应定律可得:U=
①,
由(乙)图可知:
=
②,而S=L2 ③,
由①②③式解得:U=
④,
质子在M、N间做类平抛运动,由平抛运动规律可得:
在水平方向:
d=v0t ⑤,
在竖直方向:
d=
at2 ⑥,
由牛顿第二定律和电场力公式可得:e
=ma ⑦,
由以上式子解得:v0=
⑧;
(2)质子在M、N板间做匀速直线运动,
它受到电场力和洛仑兹力这一对平衡力作用.
由平衡条件得:evB=e
⑨,
由⑨式解得:B=
,B的方向垂直纸面向外;
(3)质子恰好没有碰到P板,
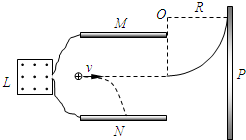
质子在磁场中做圆周运动的轨迹与P板相切,
由右图可知:evB=m
,
由几何知识知M板右端到P板的距离:S=R,
由以上两式解得S=
;
答:(1)电压为
,初速度为
;
(2)磁感应强度B=
,方向:垂直纸面向外;
(3)M板右端到P板的距离得S=
.
则由法拉第电磁感应定律可得:U=
| △Φ |
| △t |
由(乙)图可知:
| △Φ |
| △t |
| B0S |
| t0 |
由①②③式解得:U=
| B0L2 |
| t0 |
质子在M、N间做类平抛运动,由平抛运动规律可得:
在水平方向:
| 1 |
| 2 |
在竖直方向:
| 1 |
| 2 |
| 1 |
| 2 |
由牛顿第二定律和电场力公式可得:e
| U |
| d |
由以上式子解得:v0=
| L |
| 2 |
|
(2)质子在M、N板间做匀速直线运动,
它受到电场力和洛仑兹力这一对平衡力作用.
由平衡条件得:evB=e
| U |
| d |
由⑨式解得:B=
| B0L2 |
| dvt0 |
(3)质子恰好没有碰到P板,

质子在磁场中做圆周运动的轨迹与P板相切,
由右图可知:evB=m
| v2 |
| R |
由几何知识知M板右端到P板的距离:S=R,
由以上两式解得S=
| mdt0v2 |
| eB0L2 |
答:(1)电压为
| B0L2 |
| t0 |
| L |
| 2 |
|
(2)磁感应强度B=
| B0L2 |
| dvt0 |
(3)M板右端到P板的距离得S=
| mdt0v2 |
| eB0L2 |

练习册系列答案
相关题目
 如图(甲)所示,用长度均为l的两根轻软导线水平悬吊起一质量为m、长也为l的铜棒,置于磁感应强度为B方向竖直向上的匀强磁场中.未通电时,两轻导线竖直;当通入恒定电流后,铜棒向外摆动,轻导线最大偏角为θ,求铜棒中电流的大小;
如图(甲)所示,用长度均为l的两根轻软导线水平悬吊起一质量为m、长也为l的铜棒,置于磁感应强度为B方向竖直向上的匀强磁场中.未通电时,两轻导线竖直;当通入恒定电流后,铜棒向外摆动,轻导线最大偏角为θ,求铜棒中电流的大小;