题目内容
如图所示，光滑弧形轨道下端与水平传送带连接，轨道上的A点到传送带及传送带到地面的高度均为h＝5 m．把一物体自A点由静止释放，物体与传送带之间的动摩擦因数μ＝0.2。先让传送带不转动，物体滑上传送带后，从右端B点水平飞出，落在地面上的P点，B、P间的水平距离OP为x＝2 m．然后让传送带沿顺时针方向转动，速度大小为v＝5 m/s，取g＝10 m/s2.求：
(1)传送带转动时，物体落在何处？
(2)先后两种情况下，传送带对物体做功的比值．
(3)两种情况下，物体运动所用时间之差．
解析 (1)物体刚进入传送带时，由mgh＝
mv
得：v1＝10 m/s
离开B端物体做平抛运动用时t1，有h＝gt，解得：t1＝1 s
传送带静止时，物体到B端的速度v2＝
＝2 m/s
传送带转动时，因为v2＜v＜v1，故物体先减速后匀速
由v2′＝v＝5 m/s得，x′＝v2′t1＝5 m ………………………………4分
(2)第一次传送带对物体所做的功：W1＝m(v2－v)
第二次传送带对物体所做的功：W2＝m(v2－v)
两次做功之比
＝
＝
………………………………3分
(3)物体速度由10 m/s减小到5 m/s的过程，两次用时相同，传送带静止时，
物体由5 m/s减小到2 m/s用时t＝
＝1.5 s
t时间内，物体前行L＝
t＝5.25 m
传送带转动时，物体前行L用时t′＝
＝
s＝1.05 s
故第二次比第一次少用时Δt＝t－t′＝1.5 s－1.05 s＝0.45 s ………………4分
答案 (1)5 m (2) (3)0.45 s
练习册系列答案
相关题目
（2011?江苏模拟）如图所示为放置在竖直平面内游戏滑轨的模拟装置，滑轨由四部分粗细均匀的金属杆组成，其中水平直轨AB与倾斜直轨CD长均为L=6m，圆弧形轨道AQC和BPD均光滑，AQC的半径为r=1m，AB、CD与两圆弧形轨道相切，O2D、O1C与竖直方向的夹角均为θ=37°．现有一质量为m=1kg的小球穿在滑轨上，以Ek0=24J的初动能从B点开始水平向左运动，小球与两段直轨道间的动摩擦因数均为μ=
（2010?上海模拟）如图所示为放置在竖直平面内游戏滑轨的模拟装置，滑轨由四部分粗细均匀的金属杆组成，其中倾斜直轨AB与水平直轨CD长均为L=3m，圆弧形轨道APD和BQC均光滑，BQC的半径为r=1m，APD的半径为R=2m，AB、CD与两圆弧形轨道相切，O2A、O1B与竖直方向的夹角均为θ=37°．现有一质量为m=1kg的小球穿在滑轨上，以Ek0的初动能从B点开始沿AB向上运动，小球与两段直轨道间的动摩擦因数均为μ=
如图所示为放置在竖直平面内游戏滑轨的模拟装置图，滑轨由四部分粗细均匀的金属杆组成，其中水平直轨AB与倾斜直轨CD两者的长L均为6m，圆弧形轨道AQC和BPD均光滑，AQC的半径r=1m，AB、CD与两圆弧形轨道相切，O2D、O1C与竖直方向的夹角θ均为37°．现有一质量m=1kg的小球穿在滑轨上，以30J的初动能Ek0从B点开始水平向右运动，小球与两段直轨道间的动摩擦因素μ均为
如图所示为放置在竖直平面内游戏滑轨的模拟装置，滑轨由四部分粗细均匀的金属杆组成，其中倾斜直轨AB与水平直轨CD长均为L=3m，圆弧形轨道APD和BQC均光滑，AB、CD与两圆弧形轨道相切，BQC的半径为r=1m，APD的半径为R=2m，O2A、O1B与竖直方向的夹角均为θ=37°．现有一质量为m=1kg的小球穿在滑轨上，以Ek0的初动能从B点开始沿AB向上运动，小球与两段直轨道间的动摩擦因数均为μ=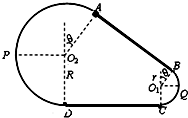
（2011?浙江模拟）如图所示为放置在竖直平面内游戏滑轨的模拟装置，滑轨由四部分粗细均匀的金属杆组成，其中倾斜直轨AB与水平直轨CD长均为L=3m，圆弧形轨道APD和BQC均光滑，BQC的半径为r=1m，APD的半径为R，AB、CD与两圆弧形轨道相切，O2A、O1B与竖直方向的夹角均为θ=370．现有一质量为m=1kg的小环穿在滑轨上，以某一初速度从B点开始沿AB向上运动，并恰能通过滑轨最高点．设小环与两段直轨道间的动摩擦因数均为