题目内容
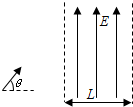 (2013?防城港模拟)如图所示,一带电粒子以某一速度在竖直平面内做直线运动,经过一段时间后进入一垂直于纸面向里、磁感应强度为B的圆形匀强磁场(图中未画出磁场区域),粒子飞出磁场后垂直电场方向进入宽为L的匀强电场,电场强度大小为E,方向竖直向上.当粒子穿出电场时速度大小变为原来的
(2013?防城港模拟)如图所示,一带电粒子以某一速度在竖直平面内做直线运动,经过一段时间后进入一垂直于纸面向里、磁感应强度为B的圆形匀强磁场(图中未画出磁场区域),粒子飞出磁场后垂直电场方向进入宽为L的匀强电场,电场强度大小为E,方向竖直向上.当粒子穿出电场时速度大小变为原来的| 2 |
(1)粒子带什么性质的电?
(2)带电粒子在磁场中运动时速度多大?
(3)圆形磁场区域的最小面积为多大?
分析:由粒子在磁场中的运动轨迹及左手定则可确定粒子的电性.因洛伦兹力对粒子不做功,则粒子进入电场做类平抛运动,将运动分解,从而求出初速度大小.由粒子在磁场中运动轨道从而求出轨道半径,并以入射点与出射点连线作为直径,得出最小圆形磁场区域.
解答:解:(1)粒子在磁场中偏转的情况和左手定则可知,粒子带负电.
(2)由于洛伦兹力对粒子不做功,故粒子以原来的速率进入电场中,
设带电粒子进入电场的初速度为v0,在电场中偏转时做类平抛运动,
由题意知粒子离开电场时的末速度大小为vt=
v0,
将vt分解为平行电场方向和垂直电场方向的两个分速度:
由几何关系知 vy=v0 vy=at
v0=
a=
F=Eq
联立以上五式求解得:v0=
(3)如图所示,带电粒子在磁场中所受到洛伦兹力作为向心力,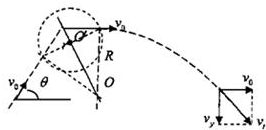
设在磁场中做圆周运动的半径为R,圆形磁场区域的半径为r,
则有:Bqv0=m
解得:R=
=
由几何关系可得:r=Rsin30°
磁场区域的最小面积为S=πr2
联立以上三式可得:S=
.
(2)由于洛伦兹力对粒子不做功,故粒子以原来的速率进入电场中,
设带电粒子进入电场的初速度为v0,在电场中偏转时做类平抛运动,
由题意知粒子离开电场时的末速度大小为vt=
| 2 |
将vt分解为平行电场方向和垂直电场方向的两个分速度:
由几何关系知 vy=v0 vy=at
v0=
| L |
| t |
| F |
| m |
联立以上五式求解得:v0=
|
(3)如图所示,带电粒子在磁场中所受到洛伦兹力作为向心力,

设在磁场中做圆周运动的半径为R,圆形磁场区域的半径为r,
则有:Bqv0=m
| ||
| R |
解得:R=
| mv0 |
| Bq |
| 1 |
| B |
|
由几何关系可得:r=Rsin30°
磁场区域的最小面积为S=πr2
联立以上三式可得:S=
| πmEL |
| 4B2q |
点评:本题考查带电粒子在电场、磁场中两运动模型:匀速圆周运动与类平抛运动,及相关的综合分析能力,以及空间想像的能力,应用数学知识解决物理问题的能力.

练习册系列答案
相关题目
 (2013?防城港模拟)如图所示,导热性能良好的气缸内用活塞封闭一定质量的空气,气缸固定不动.一条细线左端连接在活塞上,另一端跨过定滑轮后连接在一个小桶上,开始时活塞静止.现不断向小桶中添加细沙,使活塞缓慢向右移动(活塞始终未被拉出气缸).则在活塞移动过程中,下列说法正确的是( )
(2013?防城港模拟)如图所示,导热性能良好的气缸内用活塞封闭一定质量的空气,气缸固定不动.一条细线左端连接在活塞上,另一端跨过定滑轮后连接在一个小桶上,开始时活塞静止.现不断向小桶中添加细沙,使活塞缓慢向右移动(活塞始终未被拉出气缸).则在活塞移动过程中,下列说法正确的是( )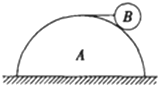 (2013?防城港模拟)如图所示,质量为M、半径为R的半球形物体A放在水平地面上,通过最高点处的钉子用水平细线拉住一质量为m、半径为r的光滑球B.则( )
(2013?防城港模拟)如图所示,质量为M、半径为R的半球形物体A放在水平地面上,通过最高点处的钉子用水平细线拉住一质量为m、半径为r的光滑球B.则( ) (2013?防城港模拟)一半径为R的半圆形玻璃砖放置在竖直平面上,其截面如下图所示.图中O为圆心,MN为竖直方向的直径.有一束细光线自O点沿水平方向射入玻璃砖,可以观测到有光线自玻璃砖内射出,现将入射光线缓慢平行下移,当入射光线与O点的距离为d时,从玻璃砖射出的光线刚好消失.则此玻璃的折射率为( )
(2013?防城港模拟)一半径为R的半圆形玻璃砖放置在竖直平面上,其截面如下图所示.图中O为圆心,MN为竖直方向的直径.有一束细光线自O点沿水平方向射入玻璃砖,可以观测到有光线自玻璃砖内射出,现将入射光线缓慢平行下移,当入射光线与O点的距离为d时,从玻璃砖射出的光线刚好消失.则此玻璃的折射率为( ) (2013?防城港模拟)如图所示,固定的光滑圆弧轨道ABC的半径为0.8m,A点与圆心O在同一水平线上,圆弧轨道底端B点与圆心在同一竖直线上.C点离B点的竖直高度为0.2m,物块从轨道上的A点由静止释放,滑过B点后进入足够长的水平传送带,传送带由电动机驱动按图示方向运转,不计物块通过轨道与传送带交接处的动能损失,物块与传送带间的动摩擦因数为0.1,g取10m/s2.
(2013?防城港模拟)如图所示,固定的光滑圆弧轨道ABC的半径为0.8m,A点与圆心O在同一水平线上,圆弧轨道底端B点与圆心在同一竖直线上.C点离B点的竖直高度为0.2m,物块从轨道上的A点由静止释放,滑过B点后进入足够长的水平传送带,传送带由电动机驱动按图示方向运转,不计物块通过轨道与传送带交接处的动能损失,物块与传送带间的动摩擦因数为0.1,g取10m/s2.