题目内容
16. 如图所示,足够长的光滑金属导轨MN、PQ平行放置,宽度为L,与水平面成夹角θ,在导轨的最上端M、P之间接有电阻R,金属棒ab电阻为r,质量m,不计其他电阻.整个装置放在匀强磁场中,磁场方向垂直导轨平面向下,棒在沿斜面向上的恒力F作用下加速上升L达到最大速度v,则( )
如图所示,足够长的光滑金属导轨MN、PQ平行放置,宽度为L,与水平面成夹角θ,在导轨的最上端M、P之间接有电阻R,金属棒ab电阻为r,质量m,不计其他电阻.整个装置放在匀强磁场中,磁场方向垂直导轨平面向下,棒在沿斜面向上的恒力F作用下加速上升L达到最大速度v,则( )| A. | 在此过程中通过R的电荷量为$\frac{B{L}^{2}R}{R+r}$ | |
| B. | 当棒达到最大速度时,棒两端的电势差为Uab=$\frac{BLvR}{R+r}$ | |
| C. | 当棒达到最大速度时,回路中的感应电流I=$\frac{BLv}{R+r}$ | |
| D. | 在此过程中电阻R上消耗的能量为FL-mgLsinθ |
分析 电荷量根据q=$\frac{△Φ}{R+r}$求解.棒两端的电势差等于R两端的电势差,由感应电动势公式和欧姆定律结合求解.根据能量守恒求电阻R上消耗的能量.
解答 解:A、通过R的电荷量为 q=$\overline{I}$△t=$\frac{\overline{E}}{R+r}$△t=$\frac{△Φ}{R+r}$=$\frac{B{L}^{2}}{R+r}$,故A错误.
B、当棒达到最大速度时,棒产生的感应电动势为 E=BLv,棒两端的电势差 Uab=$\frac{R}{R+r}$E=$\frac{BLvR}{R+r}$,故B正确.
C、当棒达到最大速度时,回路中的感应电流I=$\frac{E}{R+r}$=$\frac{BLv}{R+r}$,故C正确.
D、在此过程中电阻R上消耗的能量为 E=$\frac{R}{R+r}$(FL-mgLsinθ-$\frac{1}{2}m{v}^{2}$).故D错误.
故选:BC.
点评 本题求电荷量时运用q=$\frac{△Φ}{R+r}$,这是一个经验公式,做选择题可直接应用,但在计算题中要会推导.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
6.关于黑体辐射的实验规律叙述正确的有( )
| A. | 随着温度的升高,各种波长的辐射强度都有增加 | |
| B. | 随着温度的升高,辐射强度的极大值向波长较短的方向移动 | |
| C. | 黑体辐射的强度与波长无关 | |
| D. | 黑体辐射无任何实验规律 |
7. 如图所示,电厂发电机的端电压为U1=250V,输出功率为P1=10kW,在进行远距离输电时,先用理想变压器升压,再经过电阻为R线=5Ω的输电线,则下列说法中正确的是( )
如图所示,电厂发电机的端电压为U1=250V,输出功率为P1=10kW,在进行远距离输电时,先用理想变压器升压,再经过电阻为R线=5Ω的输电线,则下列说法中正确的是( )
 如图所示,电厂发电机的端电压为U1=250V,输出功率为P1=10kW,在进行远距离输电时,先用理想变压器升压,再经过电阻为R线=5Ω的输电线,则下列说法中正确的是( )
如图所示,电厂发电机的端电压为U1=250V,输出功率为P1=10kW,在进行远距离输电时,先用理想变压器升压,再经过电阻为R线=5Ω的输电线,则下列说法中正确的是( )| A. | 若用250V的低压直接输电,用户的电压只有150V | |
| B. | 若用2500V的高压输电,输电线的损耗功率仅为直接输电损耗功率的1% | |
| C. | 若用户电压220V,则升压变压器匝数比为1:10,降压变压器匝数比为10:1 | |
| D. | 若用户电压220V,则升压变压器匝数比为1:100,降压变压器匝数比为100:1 |
4.质量为m的木块静止在光滑水平面上,受到水平恒力F的作用,经过时间t,木块的位移为s,在t时刻,外力F的瞬时功率为( )
| A. | $\frac{sF}{t}$ | B. | $\frac{2sF}{t}$ | C. | $\frac{F}{m}\sqrt{2Fms}$ | D. | $\frac{F}{2m}\sqrt{Fms}$ |
11.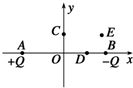 真空中某处,在x轴上关于O点对称的A、B两点有等量异种点电荷+Q和-Q,两点电荷形成的电场中分布着C、D、E三点(如图所示),其中OC=OD、BE=BD,则下列判断正确的是( )
真空中某处,在x轴上关于O点对称的A、B两点有等量异种点电荷+Q和-Q,两点电荷形成的电场中分布着C、D、E三点(如图所示),其中OC=OD、BE=BD,则下列判断正确的是( )
 真空中某处,在x轴上关于O点对称的A、B两点有等量异种点电荷+Q和-Q,两点电荷形成的电场中分布着C、D、E三点(如图所示),其中OC=OD、BE=BD,则下列判断正确的是( )
真空中某处,在x轴上关于O点对称的A、B两点有等量异种点电荷+Q和-Q,两点电荷形成的电场中分布着C、D、E三点(如图所示),其中OC=OD、BE=BD,则下列判断正确的是( )| A. | 比较电场强度的大小有EC<ED | |
| B. | 比较电势高低有φD>φE | |
| C. | 比较电势高低有φD=φE | |
| D. | 将同一正电荷从O点移到D点电场力所做的功大于从C点移到E点电场力所做的功 |
1.下列说法正确的是( )
| A. | 分子力做正功则分子势能一定减少,分子力做负功则分子势能一定增加 | |
| B. | 布朗运动是由于液体各部分温度不同引起的 | |
| C. | 物体内能只跟物体的温度有关 | |
| D. | 气体对外界做功,气体的内能可能增加 |
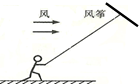
8.如图,当风水平吹来时,风筝面与水平面成一夹角,人站在地面上拉住连接风筝的细线.则( )

| A. | 空气对风筝的作用力方向垂直风筝面向上 | |
| B. | 地面对人的摩擦力方向水平向左 | |
| C. | 地面对人的支持力大小等于人和风筝的总重力 | |
| D. | 风筝处于稳定状态时拉直的细线可能垂直于风筝面 |
5. 如图所示,直径为d的纸筒绕垂直于纸面的O轴匀速转动(图示为截面).从枪口射出的子弹以速度v沿直径穿过圆筒,若子弹穿过圆筒时先后在筒上留下a、b两个弹孔.则圆筒转动的角速度ω可能为( )
如图所示,直径为d的纸筒绕垂直于纸面的O轴匀速转动(图示为截面).从枪口射出的子弹以速度v沿直径穿过圆筒,若子弹穿过圆筒时先后在筒上留下a、b两个弹孔.则圆筒转动的角速度ω可能为( )
 如图所示,直径为d的纸筒绕垂直于纸面的O轴匀速转动(图示为截面).从枪口射出的子弹以速度v沿直径穿过圆筒,若子弹穿过圆筒时先后在筒上留下a、b两个弹孔.则圆筒转动的角速度ω可能为( )
如图所示,直径为d的纸筒绕垂直于纸面的O轴匀速转动(图示为截面).从枪口射出的子弹以速度v沿直径穿过圆筒,若子弹穿过圆筒时先后在筒上留下a、b两个弹孔.则圆筒转动的角速度ω可能为( )| A. | $\frac{θ}{d}$v | B. | $\frac{π-θ}{d}$v | C. | $\frac{3π+θ}{d}$v | D. | $\frac{2π+θ}{d}$v |
6.在物理学发展历史中,许多物理学家做出了卓越贡献.以下关于物理学家所作科学贡献的叙述中,正确的是( )
| A. | 牛顿建立了相对论 | |
| B. | 伽利略提出了“日心说” | |
| C. | 卡文迪许首次比较精确地测出引力常量 | |
| D. | 开普勒发现了行星运动三定律 |