题目内容
【题目】光滑水平面上放有如图所示的用绝缘材料制成的“┙”型滑板（平面部分足够长），质量为4m，距滑板的A壁为L1距离的B处放有一质量为m，电量为+q的大小不计的小物体，小物体与板面的摩擦不计，整个装置处于场强为E、方向为水平向右的匀强电场中，初始时刻，滑板与小物体都静止，试求：
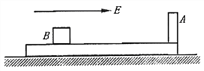
（1）释放小物体，第一次与滑板A壁碰前小物体的速度v1多大？
（2）若小物体与A壁碰后相对水平面的速度大小为碰前的
，则小物体在第二次跟A壁碰撞之前瞬时，滑板的速度v和物体的速度v2分别为多大？（均指对地速度）
（3）从小物体开始运动到第二次碰撞前的过程中，电场力做功为多大？（碰撞时间可忽略）
【答案】（1）
（2）
； 
（3）
【解析】（1）由动能定理得 qEL1=
mv12
得 
（2）若物体碰后仍沿原来方向运动，碰后滑板的速度为v，由动量守恒得
mv1=m
v1+4mv
解得， 
，由于B与A同向运动，故不可能，
∴物块碰后必反弹，速度为v1′=-
v1
根据动量守恒定律得 mv1=-m
v1+4mv
解得
由于碰后滑板匀速运动直至与物体第二碰撞之前，故物体与A第二次碰前，滑板的速度为 
物体与A壁第二碰前，设物块的速度为v2，v2=v1′+at
两物体第二次相碰时，位移相等，则有
vt=v1′t+
at2
得 v=v1′+
at，
又
联立解得， 
（3）设物体在两次碰撞之间位移为S
由
练习册系列答案
冲刺100分1号卷系列答案
相关题目
