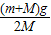题目内容
 质量为m的A球与质量为M的B球,分别连接在轻质弹簧的两端,如图所示,B球用平行于斜面的细线固定在倾角为30°的光滑斜面上,A、B球处于静止状态,当细线被剪断的瞬间,A、B两球的加速度大小分别为
质量为m的A球与质量为M的B球,分别连接在轻质弹簧的两端,如图所示,B球用平行于斜面的细线固定在倾角为30°的光滑斜面上,A、B球处于静止状态,当细线被剪断的瞬间,A、B两球的加速度大小分别为
- A.
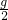 ,
,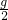
- B.0,
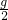
- C.0,
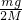
- D.0,
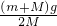
D
分析:根据共点力平衡求出弹簧的弹力大小,剪断细线的瞬间,弹簧的弹力不变,根据牛顿第二定律求出A、B两球的瞬时加速度.
解答:对 A分析,A受重力、支持力和弹簧的弹力处于平衡,根据共点力平衡知,弹簧的弹力F=mgsin30°=0.5mg,剪断细线的瞬间,弹簧的弹力不变,对A分析,A的瞬时加速度为零,对B分析,根据牛顿第二定律得,a=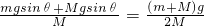 .故D正确,A、B、C错误.
.故D正确,A、B、C错误.
故选D.
点评:解决本题的关键能够正确地受力分析,运用牛顿第二定律进行求解.
分析:根据共点力平衡求出弹簧的弹力大小,剪断细线的瞬间,弹簧的弹力不变,根据牛顿第二定律求出A、B两球的瞬时加速度.
解答:对 A分析,A受重力、支持力和弹簧的弹力处于平衡,根据共点力平衡知,弹簧的弹力F=mgsin30°=0.5mg,剪断细线的瞬间,弹簧的弹力不变,对A分析,A的瞬时加速度为零,对B分析,根据牛顿第二定律得,a=
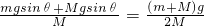 .故D正确,A、B、C错误.
.故D正确,A、B、C错误.故选D.
点评:解决本题的关键能够正确地受力分析,运用牛顿第二定律进行求解.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
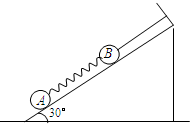 质量为m的A球与质量为M的B球,分别连接在轻质弹簧的两端,如图所示,B球用平行于斜面的细线固定在倾角为30°的光滑斜面上,A、B球处于静止状态,当细线被剪断的瞬间,A、B两球的加速度大小分别为( )
质量为m的A球与质量为M的B球,分别连接在轻质弹簧的两端,如图所示,B球用平行于斜面的细线固定在倾角为30°的光滑斜面上,A、B球处于静止状态,当细线被剪断的瞬间,A、B两球的加速度大小分别为( )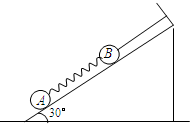

 ,
,