题目内容
高台滑雪运动员经过一段滑行后从斜坡上O点水平飞出,斜坡与水平面的夹角θ=37°,运动员连同滑雪板的总质量m=50kg,他落到了斜坡上的A点,A点与O点的距离s=12m,如图所示。忽略斜坡的摩擦和空气阻力的影响,重力加速度g=10m/s2。
(sin37°=0.60;cos37°=0.80)
(1)运动员在空中飞行了多长时间?
(2)求运动员离开O点时的速度大小。
(3)运动员落到斜坡上顺势屈腿以缓冲,使他垂直于斜坡的速度在t=0.50s的时间内减小为零,设缓冲阶段斜坡对运动员的弹力可以看作恒力,求此弹力的大小。
解:(1)设运动员在空中飞行时间为t,运动员在竖直方向做自由落体运动,得
ssin37°=gt2,
解得: t==1.2s。
(2)设运动员离开O点的速度为v0,运动员在水平方向做匀速直线运动,即
scos37°=v0t,
解得: v0==8.0m/s。
(3)运动员落在A点时沿竖直向下的速度vy的大小为
vy=gt=12m/s
沿水平方向的速度vx的大小为 vx=8.0m/s。
因此,运动员垂直于斜面向下的速度vN为
vN=vycos37°-vxsin37°=4.8m/s。
设运动员在缓冲的过程中受到斜面的弹力为N,根据牛顿第二定律
(N-mgcos37°)=mvN/t,
解得: N=mgcos37°+=880N。
解析:略

练习册系列答案
相关题目
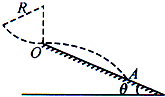 如图所示,是某跳台滑雪的雪道示意简化图,高台滑雪运动员经过一段竖直平面内的圆弧后,从圆弧所在圆的最低点O水平飞出,圆弧半径R=10m.一滑雪运动员连同滑雪板的总质量为50kg,从圆弧轨道上距O点竖直高度为3R/5处静止下滑,经过圆弧上的O点时受到的支持力大小为1000N,飞出后经时间t=2s着陆在雪道上的A点.忽略空气阻力,取重力加速度g=10m/s2.求:
如图所示,是某跳台滑雪的雪道示意简化图,高台滑雪运动员经过一段竖直平面内的圆弧后,从圆弧所在圆的最低点O水平飞出,圆弧半径R=10m.一滑雪运动员连同滑雪板的总质量为50kg,从圆弧轨道上距O点竖直高度为3R/5处静止下滑,经过圆弧上的O点时受到的支持力大小为1000N,飞出后经时间t=2s着陆在雪道上的A点.忽略空气阻力,取重力加速度g=10m/s2.求: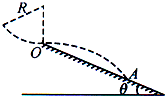 (2011?重庆模拟)如图所示,是某跳台滑雪的雪道示意简化图,高台滑雪运动员经过一段竖直平面内的圆弧后,从圆弧所在圆的最低点O水平飞出,圆弧半径R=10m.一滑雪运动员连同滑雪板的总质量为50kg,从圆弧轨道上距O点竖直高度为
(2011?重庆模拟)如图所示,是某跳台滑雪的雪道示意简化图,高台滑雪运动员经过一段竖直平面内的圆弧后,从圆弧所在圆的最低点O水平飞出,圆弧半径R=10m.一滑雪运动员连同滑雪板的总质量为50kg,从圆弧轨道上距O点竖直高度为 (2006?南汇区二模)高台滑雪运动员经过一段滑行后从斜坡上的O点水平飞出,斜坡与水平面的夹角θ=37°,运动员连同滑雪板的总质量m=50kg,他落到了斜坡上的A点,A点与O点的距离s=12m,如图所示.忽略斜坡的摩擦和空气阻力的影响,重力加速度g=10m/s2.(sin37°=0.6;cos37°=0.80)
(2006?南汇区二模)高台滑雪运动员经过一段滑行后从斜坡上的O点水平飞出,斜坡与水平面的夹角θ=37°,运动员连同滑雪板的总质量m=50kg,他落到了斜坡上的A点,A点与O点的距离s=12m,如图所示.忽略斜坡的摩擦和空气阻力的影响,重力加速度g=10m/s2.(sin37°=0.6;cos37°=0.80)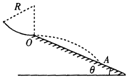 高台滑雪运动员经过一段弧长为s=
高台滑雪运动员经过一段弧长为s=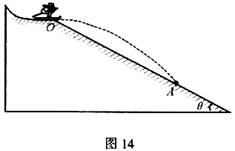 高台滑雪运动员经过一段滑行后从斜坡上的O点水平飞出,斜坡与水平面的夹角θ=37°,运动员连同滑雪板的总质量m=50kg,他落到了斜坡上的A点,A点与O点的距离s=12m,如图14所示。忽略斜坡的摩擦和空气阻力的影响,重力加速度g=10m/s2。
高台滑雪运动员经过一段滑行后从斜坡上的O点水平飞出,斜坡与水平面的夹角θ=37°,运动员连同滑雪板的总质量m=50kg,他落到了斜坡上的A点,A点与O点的距离s=12m,如图14所示。忽略斜坡的摩擦和空气阻力的影响,重力加速度g=10m/s2。