题目内容
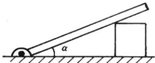 如图所示,均匀光滑直棒一端铰于地面,另一端搁在一个立方体上,杆与水平面间的夹角α为30°左右.现将立方体缓慢向左移动,则棒对立方体的压力大小将
如图所示,均匀光滑直棒一端铰于地面,另一端搁在一个立方体上,杆与水平面间的夹角α为30°左右.现将立方体缓慢向左移动,则棒对立方体的压力大小将
- A.逐渐增大
- B.逐渐减小
- C.先增大后减小
- D.先减小后增大
C
分析:在立方体缓慢向左推的过程中,棒处于力矩平衡状态;棒受重力力矩及立方体对棒的压力力矩而处于平衡,根据力矩平衡条件列式,通过重力力矩变化即可得出压力力矩的变化,从而解出压力的变化.
解答:设棒的重力大小为G,立方体对棒的弹力(方向与棒垂直斜向上)大小为F,棒的长度为L,重心在棒的中点,立方体的边长为h,棒与地面之间的夹角为α,根据力矩平衡条件得:
G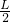 cosα=F
cosα=F
因α增大,cosα减小,故Gcosα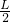 减小,所以立方体对棒的压力力矩减小;
减小,所以立方体对棒的压力力矩减小;
由上式解得:
F= sin2α
sin2α
由数学知识可知,当θ=45°时,F有最大值
所以立方体缓慢向左推时,立方体对棒的压力F先增大,后减小;
故选:C
点评:本题考查了力矩平衡条件的应用,解题的关键在于分析题目中力臂的变化,列出力矩平衡方程;同时要注意能灵活转换思维,能用重力的力矩表示出压力力矩的变化.
分析:在立方体缓慢向左推的过程中,棒处于力矩平衡状态;棒受重力力矩及立方体对棒的压力力矩而处于平衡,根据力矩平衡条件列式,通过重力力矩变化即可得出压力力矩的变化,从而解出压力的变化.
解答:设棒的重力大小为G,立方体对棒的弹力(方向与棒垂直斜向上)大小为F,棒的长度为L,重心在棒的中点,立方体的边长为h,棒与地面之间的夹角为α,根据力矩平衡条件得:
G
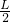 cosα=F
cosα=F
因α增大,cosα减小,故Gcosα
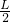 减小,所以立方体对棒的压力力矩减小;
减小,所以立方体对棒的压力力矩减小;由上式解得:
F=
 sin2α
sin2α由数学知识可知,当θ=45°时,F有最大值
所以立方体缓慢向左推时,立方体对棒的压力F先增大,后减小;
故选:C
点评:本题考查了力矩平衡条件的应用,解题的关键在于分析题目中力臂的变化,列出力矩平衡方程;同时要注意能灵活转换思维,能用重力的力矩表示出压力力矩的变化.

练习册系列答案
相关题目
 (2011?徐汇区模拟)如图所示,均匀光滑直棒一端用铰链装在水平地面上,另一端搁在立方体上,棒与地面夹角α为30°左右,现将立方体缓慢向左推,则立方体对棒的压力力矩变化情况为
(2011?徐汇区模拟)如图所示,均匀光滑直棒一端用铰链装在水平地面上,另一端搁在立方体上,棒与地面夹角α为30°左右,现将立方体缓慢向左推,则立方体对棒的压力力矩变化情况为 (2011?上海模拟)如图所示,均匀光滑直棒一端铰于地面,另一端搁在一个立方体上,杆与水平面间的夹角α为30°左右.现将立方体缓慢向左移动,则棒对立方体的压力大小将( )
(2011?上海模拟)如图所示,均匀光滑直棒一端铰于地面,另一端搁在一个立方体上,杆与水平面间的夹角α为30°左右.现将立方体缓慢向左移动,则棒对立方体的压力大小将( )
 与h关系图线.请写出杆绕O点转动时的动能Ek与vA的关系式;
与h关系图线.请写出杆绕O点转动时的动能Ek与vA的关系式;

