题目内容
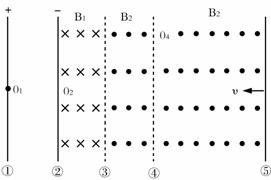
如图所示,①②为两平行金属板,③为方向相反的两个匀强磁场的分界线,④为过O4点的一条虚线.①②③④相互平行,间距均为![]() ,其中在①和②间加有
,其中在①和②间加有![]() 的电压,已知磁感应强度的大小
的电压,已知磁感应强度的大小![]() ,方向如图,现从金属板中点O1的附近由静止释放一质量
,方向如图,现从金属板中点O1的附近由静止释放一质量![]() 、电荷量
、电荷量![]() 的粒子,粒子被电场加速后穿过小孔O2再经过磁场B1、B2偏转后,通过O4点,不计粒子重力,(计算结果都保留两位有效数字),试求:
的粒子,粒子被电场加速后穿过小孔O2再经过磁场B1、B2偏转后,通过O4点,不计粒子重力,(计算结果都保留两位有效数字),试求:
(1)粒子从O1运动到O4的时间;
(2)若粒子刚开始释放时,右方距分界线④40m处有一与之平行的挡板⑤正向左以速度![]() 匀速移动,当与粒子相遇时粒子运动方向恰好与挡板平行,求
匀速移动,当与粒子相遇时粒子运动方向恰好与挡板平行,求![]() 的大小.
的大小.
解:(1)根据动能定理,在加速过程中有:![]()
粒子在匀强磁场B1中做匀速圆周运动,有:![]()
由以上二式解得 ![]()
设粒子在匀强磁场B1中的运动轨迹所对应的圆心角为![]() ,由几何关系可知:
,由几何关系可知:
![]() ,所以
,所以![]()
根据题意和几何知识可知,粒子在匀强磁场B2中的运动轨迹所对应的圆心角也为![]() ,到达O4点时,粒子的速度方向恰好水平向右,此后粒子继续在匀强磁场B2中做匀速圆周运动,再回到匀强磁场B1中做匀速圆周运动,由于粒子做匀速圆周运动的圆心不在O1O2的延长线上,所以粒子不会回到O2点,运动也失去了周期性.
,到达O4点时,粒子的速度方向恰好水平向右,此后粒子继续在匀强磁场B2中做匀速圆周运动,再回到匀强磁场B1中做匀速圆周运动,由于粒子做匀速圆周运动的圆心不在O1O2的延长线上,所以粒子不会回到O2点,运动也失去了周期性.
粒子在匀强磁场中做匀速圆周运动的周期:![]()
金属板①②间匀强电场的场强为:![]()
粒子在匀强电场中运动的加速度为:![]()
设粒子从O1直接运动到O2所用的时间为![]() ,则:
,则:![]()
解得:![]()
所以粒子从![]() 到
到![]() 运动的时间为:
运动的时间为:![]()
(2)板⑤的移动时间为:![]()
板⑤移动的距离为:![]()
板⑤移动的速度为:![]()

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 (2010?长春一模)如图所示,C为两极板水平放置的平行板电容器,闭合开关S,当滑动变阻器R1、R2的滑片处于各自的中点位置时,悬在电容器C两极板间的带电尘埃P恰好处于静止状态,要使尘埃P向下加速运动,下列方法中可行的是( )
(2010?长春一模)如图所示,C为两极板水平放置的平行板电容器,闭合开关S,当滑动变阻器R1、R2的滑片处于各自的中点位置时,悬在电容器C两极板间的带电尘埃P恰好处于静止状态,要使尘埃P向下加速运动,下列方法中可行的是( ) 如图所示,C为两极板水平放置的平行板电容器,闭合开关S,当滑动变阻器R1、R2的滑片处于各自的中点位置时,悬在电容器C两极板间的带电尘埃P恰好处于静止状态.现要使尘埃P向上加速运动,下列方法中可行是( )
如图所示,C为两极板水平放置的平行板电容器,闭合开关S,当滑动变阻器R1、R2的滑片处于各自的中点位置时,悬在电容器C两极板间的带电尘埃P恰好处于静止状态.现要使尘埃P向上加速运动,下列方法中可行是( )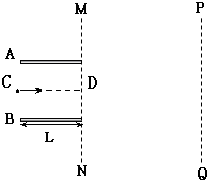 如图所示,AB为一对平行板,板间存在匀强电场,板长L=16cm,两板间距离d=16cm,两板间电势差UAB=+1200V.带电粒子的电荷量为q=+1.0×10-10C、质量m=1.0×10-20kg,该粒子沿电场中心线CD以初速度υ0=4×106m/s垂直电场线射入电场.AB板右侧MN、PQ区域存在水平向右的匀强电场,MN与PQ间的电势差为1200V(粒子的重力不计)
如图所示,AB为一对平行板,板间存在匀强电场,板长L=16cm,两板间距离d=16cm,两板间电势差UAB=+1200V.带电粒子的电荷量为q=+1.0×10-10C、质量m=1.0×10-20kg,该粒子沿电场中心线CD以初速度υ0=4×106m/s垂直电场线射入电场.AB板右侧MN、PQ区域存在水平向右的匀强电场,MN与PQ间的电势差为1200V(粒子的重力不计)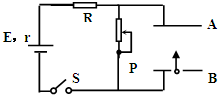 如图所示电路中,两平行板A、B水平放置,两板间距离d=40cm,电源电动势E=24V,内电阻r=1Ω,电阻R=15Ω.闭合开关s,待电路稳定后,将一带正电的小球从B板小孔以初速度v0=4m/s竖直向上射入板间.小球带电量为q=10-2C,质量为m=2×10-2kg,不考虑空气阻力.若调节滑动变阻器,使小球恰能达到A板,则电源的输出功率为( )(g=10m/s2)
如图所示电路中,两平行板A、B水平放置,两板间距离d=40cm,电源电动势E=24V,内电阻r=1Ω,电阻R=15Ω.闭合开关s,待电路稳定后,将一带正电的小球从B板小孔以初速度v0=4m/s竖直向上射入板间.小球带电量为q=10-2C,质量为m=2×10-2kg,不考虑空气阻力.若调节滑动变阻器,使小球恰能达到A板,则电源的输出功率为( )(g=10m/s2)