题目内容
如图所示,一劲度系数为k的轻弹簧左端固定在长且薄的木板A的左端,轻弹簧右端与小物块B连接,已知木板A的质量为mA,小物块B的质量为mB,且A、B之间以及A与水平地面间均光滑.开始时,A和B均静止,现同时对A、B施加等大反向的水平恒力F1和F2,即F1=F2=F.设整个过程中弹簧的形变不超过其弹性限度,B始终未滑离A.求:![]()
(1)以地面作为参考系,求当木板A的位移为lA时,物块B的位移lB的大小;
(2)当弹簧的伸长量最大时,木板A的位移lA′是多大?并求这时由A、B及弹簧组成的系统所具有的机械能E.
(1)由动量守恒mA![]() -mB
-mB![]() =0 ①
=0 ①
则物块B位移的大小lb=![]() . ②
. ②
(2)A、B做同频率的简谐运动,设运动到平衡位置时弹簧的伸长量为x,有F=kx ③
弹簧的伸长量最大时,有lA′+lB′=2x ④
由动量守恒可推知mAlA′-mBlB′=0 ⑤
联立求解,得弹簧的伸长量最大时lA′=![]() ⑥
⑥
这时系统具有的机械能E=![]() . ⑦
. ⑦

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
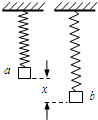 如图所示,一劲度系数为k的弹簧,下端悬挂一质量为m的重物,平衡时物体在a位置.现用力将物体向下拉长x至b位置,则此时弹簧的弹力为( )
如图所示,一劲度系数为k的弹簧,下端悬挂一质量为m的重物,平衡时物体在a位置.现用力将物体向下拉长x至b位置,则此时弹簧的弹力为( )| A、kx | B、mg+kx | C、mg-kx | D、以上说法都不正确 |
 (2013?朝阳区模拟)如图所示,一劲度系数为k的轻弹簧,上端固定在天花板上,下端悬挂木块A.木块A处于静止状态时弹簧的伸长为△l(弹簧的形变在弹性限度内),则木块A所受重力的大小等于( )
(2013?朝阳区模拟)如图所示,一劲度系数为k的轻弹簧,上端固定在天花板上,下端悬挂木块A.木块A处于静止状态时弹簧的伸长为△l(弹簧的形变在弹性限度内),则木块A所受重力的大小等于( ) 如图所示,一劲度系数k=800N/m的轻弹簧的两端各焊接着两个质量均为m=12kg的物体A、B,A、B和轻弹簧静止竖立在水平地面上.现加一竖直向上的力F在上面的物体A上,使物体A开始向上做匀加速运动,经0.4s物体B刚要离开地面,设整个过程中弹簧都处于弹性限度内,取g=10m/s2.求:
如图所示,一劲度系数k=800N/m的轻弹簧的两端各焊接着两个质量均为m=12kg的物体A、B,A、B和轻弹簧静止竖立在水平地面上.现加一竖直向上的力F在上面的物体A上,使物体A开始向上做匀加速运动,经0.4s物体B刚要离开地面,设整个过程中弹簧都处于弹性限度内,取g=10m/s2.求: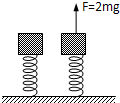 如图所示,一劲度系数为k的轻弹簧下端固定在水平地面上,上端与一质量为m的物块相连,处于静止状态,现施加一竖直向上的大小为F=2mg的恒力,求物块上升多高时物块速度最大?
如图所示,一劲度系数为k的轻弹簧下端固定在水平地面上,上端与一质量为m的物块相连,处于静止状态,现施加一竖直向上的大小为F=2mg的恒力,求物块上升多高时物块速度最大?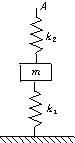 如图所示,一劲度系数为k1的弹簧,竖直地放在桌面上,上面压一质量为m的物体,另一劲度系数为k2的弹簧竖直放在物体上面,其下端与物体的上表面连接在一起,两个弹簧的质量都不计.要使下面弹簧的弹力减为原来的一半时,应将上面弹簧的上端A竖直向上提高多少?
如图所示,一劲度系数为k1的弹簧,竖直地放在桌面上,上面压一质量为m的物体,另一劲度系数为k2的弹簧竖直放在物体上面,其下端与物体的上表面连接在一起,两个弹簧的质量都不计.要使下面弹簧的弹力减为原来的一半时,应将上面弹簧的上端A竖直向上提高多少?