题目内容
【题目】如图所示，两光滑轨道相距L=0.5m，固定在倾角为
的斜面上，轨道下端接入阻值为R=1.6Ω的定值电阻。整个轨道处在竖直向上的匀强磁场中，磁感应强度B=1T。一质量m=0.1kg的金属棒MN从轨道顶端由静止释放，沿轨道下滑，金属棒沿轨道下滑x=3.6m时恰好达到最大速度（轨道足够长），在该过程中，金属棒始终能保持与轨道良好接触。（轨道及金属棒的电阻不计，重力加速度g取10m/s2, sin37° = 0.6，cos37°= 0.8)求：
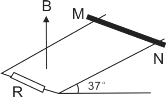
（1）金属棒下滑过程中，M、N哪端电势高；
（2）求金属棒下滑过程中的最大速度v；
（3）求该过程回路中产生的焦耳热Q。
【答案】（1）M端电势较高 （2）6m/s （3）
【解析】
（1）根据右手定则，可判知M端电势较高
（2）设金属棒的最大速度为v，根据法拉第电磁感应定律，回路中的感应电动势
E=BLvcos
根据闭合电路欧姆定律，回路中的电流强度
I=E/R
金属棒所受安培力F为
F=BIL
对金属棒，根据平衡条件列方程
mgsin=Fcos
联立以上方程解得：
v=6m/s
(3)根据能量守恒
代入数据解得：
【题目】某实验小组进行测量动摩擦因数大小实验。
⑴实验时，小明同学先在竖直方向上对弹簧测力计调零，然后用弹簧测力计拉着物体沿水平方向做匀速直线运动，那么弹簧测力计的示数与物体所受摩擦力相比_______（选填“偏大”或“偏小”）。
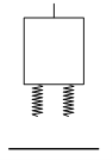
⑵弹簧测力计正确调零后，小明同学设计了如图所示两种实验方案，来测量物体A与长木板B之间的滑动摩擦力大小。
方案1：如图甲所示，把长木板B固定在水平面上，匀速拉动物体A；
方案2：如图乙所示，把长木板B放在水平面上，拉动长木板B。
以上两种实验方案，你认为方案____更为合理；这是因为___________________
⑶小王同学利用合理的实验装置进行实验。在物体A上放上橡皮泥，准确测得物体A和橡皮泥的总重量G，实验中待弹簧测力计指针稳定后，将其读数记作F。改变物体A上橡皮泥重量，重复多次，得到实验数据如表格所示：
G/N | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 |
F/N | 0.29 | 0.46 | 0.59 | 0.76 | 0.90 |
①根据表格所示实验数据，请你在答题纸的图丙中做出F-G图线____；
②由图线可以测得物体A与长木板B之间的动摩擦因数μ=________。
