题目内容
9.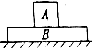 质量为mA=10千克的长方体木块A放在质量为mB=20千克的长方体木块B上,木块B放在水平地面上(见图所示).木块A和B之间的摩擦系数μ1=0.1,木块B与水平地面间的摩擦系数μ2=0.2,取10米/秒2,欲将木块B从木块A下抽出,则作用在木块B上的水平拉力F至少应多大?
质量为mA=10千克的长方体木块A放在质量为mB=20千克的长方体木块B上,木块B放在水平地面上(见图所示).木块A和B之间的摩擦系数μ1=0.1,木块B与水平地面间的摩擦系数μ2=0.2,取10米/秒2,欲将木块B从木块A下抽出,则作用在木块B上的水平拉力F至少应多大?
分析 首先B如果要能从A下面抽出,B与A势必是存在相对运动的,也就是说B和A之间存在摩擦力,算出摩擦力大小.其次由于B能从A下面抽出,B的加速度必须大于A的最大加速的加速度,否则它们之间不会存在相对运动,由牛顿第二定律列方程计算可以得到拉力F的最小值.
解答 解:如果B要能从A下面抽出,B与A势必是存在相对运动,B和A之间摩擦力大小为:f1=μ1mAg=0.1×10×10N=10N
B与地面之间的摩擦力大小为:f2=μ2(mA+mB)g=0.2×30×10N=60N
其由于B能从A下面抽出,B的加速度必须大于A的最大加速的加速度,A的最大加速度为:${a}_{1}={μ}_{1}g=1m/{s}^{2}$
因此B的最小值为:${a}_{2}=1m/{s}^{2}$
对-B由牛顿第二定律得:F+f1-f2=mBa2
解之得,拉力F的最小值为:F=70NF=70N
答:拉力F的最小值为70N
点评 此题属于相对运动的题目,关键是分析清楚A、B物体的运动情况和受力情况.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.物体以5m/s的速度匀速通过直线上的A、B两点,所用时间为2s,现在物体从A点由静止出发,先做匀加速直线运动(加速度为a1)到某一最大速度vm,然后立即做匀减速直线运动(加速度大小为a2)至B点速度恰好减为0,所用时间仍为2s.则物体的( )
| A. | vm只能为10m/s,与a1、a2的大小无关 | |
| B. | vm可为许多值,与a1、a2的大小有关 | |
| C. | a1、a2必须满足$\frac{1}{{a}_{1}}+\frac{1}{{a}_{2}}=\frac{1}{5}$s2/m | |
| D. | a1、a2必须是一定的 |
14.关于电动势E,下列说法中正确的是( )
| A. | 电动势E的大小等于单位时间内非静电力所做的功 | |
| B. | 电动势E是由电源本身决定的,跟电源的体积和外电路均无关 | |
| C. | 电动势E的单位与电势、电势差的单位都是伏特,故三者本质上一样 | |
| D. | 电动势E是表征电源把其他形式的能转化为电能本领的物理量 |
1. 有一口井,水面距井口4m,现用水桶从井中提水(如图),水桶出井后又将其提升了1m.选井口处为坐标原点,以水桶竖直向上提升的路线为x轴,向上为正方向,则水桶在水面时的位置和最后的位置坐标分别是( )
有一口井,水面距井口4m,现用水桶从井中提水(如图),水桶出井后又将其提升了1m.选井口处为坐标原点,以水桶竖直向上提升的路线为x轴,向上为正方向,则水桶在水面时的位置和最后的位置坐标分别是( )
 有一口井,水面距井口4m,现用水桶从井中提水(如图),水桶出井后又将其提升了1m.选井口处为坐标原点,以水桶竖直向上提升的路线为x轴,向上为正方向,则水桶在水面时的位置和最后的位置坐标分别是( )
有一口井,水面距井口4m,现用水桶从井中提水(如图),水桶出井后又将其提升了1m.选井口处为坐标原点,以水桶竖直向上提升的路线为x轴,向上为正方向,则水桶在水面时的位置和最后的位置坐标分别是( )| A. | 4 m,1 m | B. | -4 m,1 m | C. | 5 m,0 | D. | -5 m,1 m |
19.下列关于近代物理知识的描述中,正确的是( )
| A. | 处于n=3能级状态的大量氢原子自发跃迁时,能发出3种种频率的光子 | |
| B. | β射线实际上是原子的核外电子挣脱原子核的束缚而形成的 | |
| C. | 在${\;}_{7}^{14}$N+${\;}_{2}^{4}$He→${\;}_{8}^{17}$O+X核反应中,x是质子,这个反应过程叫α衰变 | |
| D. | 原子核所含核子单独存在时的总质量等于该原子核的质量 |