题目内容
13. 如图所示,电池组的电动势E=18V,内阻r=1Ω,R2=5Ω,R3=6Ω,平行金属板水平放置,板间距离d=2cm,当可变电阻R1的滑片移到R1的中点时,一个带电q=-8×10-7C的油滴正好平衡于平行板间,电流表示数为2A,求:
如图所示,电池组的电动势E=18V,内阻r=1Ω,R2=5Ω,R3=6Ω,平行金属板水平放置,板间距离d=2cm,当可变电阻R1的滑片移到R1的中点时,一个带电q=-8×10-7C的油滴正好平衡于平行板间,电流表示数为2A,求:(1)R1的全部电阻值;
(2)油滴的质量;
(3)在R1的滑片移动到最下端时,油滴获得的加速度是多大?
分析 (1)电路稳定后,电容器相当于断路,电路中滑动变阻器的一半阻值与R3并联后与R2串联,电容器并联在R2两端;由闭合电路欧姆定律可求得R1的一半阻值,即可求得总阻值;
(2)电容器两端的电压等于R2两端的电压,带电微粒处于悬浮状态,故受力平衡;由受力平衡可求得微粒的质量;
(3)当微粒受电场力最大时其加速度最大,则可知当R2两端的电压最大时加速度最大;分析电路的变化可知滑片的位置.
解答 解:(1)由闭合电路欧姆定律可得:
电路中的总电阻 R总=$\frac{E}{I}$-r=$\frac{18}{2}$Ω-1Ω=8Ω;
则并联部分总电阻 R并=8-5Ω=3Ω;
由并联电路的电阻规律可得:$\frac{{R}_{3}•\frac{{R}_{1}}{2}}{{R}_{3}+\frac{{R}_{1}}{2}}$=3Ω;
解得:R1=12Ω;
即滑动变阻器的总阻值为12Ω
(2)R2两端的电压 U2=IR2=2×5Ω=10V;
故电容器两端的电压为10V,由 $\frac{U}{d}$q=mg可得:
m=$\frac{qU}{gd}$=$\frac{8×1{0}^{-7}×10}{10×0.02}$=4×10-5kg;
故带电油滴的质量为4×10-5kg;
(3)要使带电微粒有最大加速度,则应使电容器两端的电压最大,即R2两端的电压最大,由串联电路的规律可知,应使并联部分电阻最小,即应使滑动变阻器短接时,此时并联部分电阻为零;
由闭合电路的欧姆定律可知,R2两端的最大电压 Um=$\frac{E}{r+{R}_{2}}$R2=$\frac{18}{1+5}$×5V=15V
此时粒子受电场力 F=$\frac{q{U}_{m}}{d}$
加速度 a=$\frac{F-mg}{m}$=5m/s2;
带电粒子的最大加速度为5m/s2.
答:
(1)R1的全部电阻值是12Ω;
(2)油滴的质量是4×10-5kg;
(3)在R1的滑片移动到最下端时,油滴获得的加速度是5m/s2.
点评 本题综合考查了闭合电路的欧姆定律、电容器、牛顿第二定律等重点知识,综合性较强;解题时注意寻找到各知识点及它们之间的联系,特别是要注意电路的分析及电容器的性质.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案 放置在光滑地面上的物体,在某种力的作用下从静止开始做直线运动,如果该物体的速度一时间图象是一条抛物线,如图所示,则下列说法正确的是( )
放置在光滑地面上的物体,在某种力的作用下从静止开始做直线运动,如果该物体的速度一时间图象是一条抛物线,如图所示,则下列说法正确的是( )| A. | 0~t1内物体做匀加速直线运动 | |
| B. | t1时刻物体的速度最大,加速度也最大 | |
| C. | 物体在0~t1内和t1~t2内运动的位移相等 | |
| D. | 物体在0~t1内和t1~t2内运动的速度方向相同 |
| A. | 可以定点在我国的上空 | B. | 运行周期是24 h | ||
| C. | 加速度等于9.8 m/s2 | D. | 运行速度小于7.9 km/s |
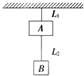
| A. | L1对A的拉力和L2对A的拉力是一对平衡力 | |
| B. | L2对A的拉力和L2对B的拉力是一对作用力与反作用力 | |
| C. | L2对B的拉力和B的重力是一对平衡力 | |
| D. | L2对B的拉力和B对L2的拉力是一对作用力和反作用力 |
| A. | 3m/s2 | B. | 5m/s2 | C. | 8m/s2 | D. | 10m/s2 |
 如图所示,实线记录了一次实验中得到的运动小车的v-t图象,为了简化计算,用虚线作近似处理,下列表述正确的是( )
如图所示,实线记录了一次实验中得到的运动小车的v-t图象,为了简化计算,用虚线作近似处理,下列表述正确的是( )| A. | 小车做曲线运动 | |
| B. | 小车先做加速运动,再匀速运动,最后做减速运动 | |
| C. | 在t1时刻虚线反映的加速度比实际小 | |
| D. | 在0~t1的时间内,由虚线计算出的平均速度比实际的小 |


 如图所示,匀强电场中A、B、C三点构成一个直角三角形中,∠A=30°,边长AC=32$\sqrt{3}$cm.把电荷量q=-2×10-10C的点电荷由A点移到B点,电场力做功4.8×10-8J,再由B点移到C点,电荷克服电场力做功4.8×10-8J,取B点的电势为零,求
如图所示,匀强电场中A、B、C三点构成一个直角三角形中,∠A=30°,边长AC=32$\sqrt{3}$cm.把电荷量q=-2×10-10C的点电荷由A点移到B点,电场力做功4.8×10-8J,再由B点移到C点,电荷克服电场力做功4.8×10-8J,取B点的电势为零,求 如图所示,一轻质弹簧两端连着物体A和B,静止放在光滑水平地面上,物体A的质量为190g,物体B的质量为600g.一质量为10g的子弹以400m/s的速度水平击中物体A并嵌在其中,试求:
如图所示,一轻质弹簧两端连着物体A和B,静止放在光滑水平地面上,物体A的质量为190g,物体B的质量为600g.一质量为10g的子弹以400m/s的速度水平击中物体A并嵌在其中,试求: