题目内容
19. 如图所示,一轻质弹簧两端连着物体A和B,静止放在光滑水平地面上,物体A的质量为190g,物体B的质量为600g.一质量为10g的子弹以400m/s的速度水平击中物体A并嵌在其中,试求:
如图所示,一轻质弹簧两端连着物体A和B,静止放在光滑水平地面上,物体A的质量为190g,物体B的质量为600g.一质量为10g的子弹以400m/s的速度水平击中物体A并嵌在其中,试求:(1)子弹击中A后的瞬间,物体A的速度vA;
(2)在以后的运动过程中,弹簧被拉伸得最长时,物体B的速度vB;
(3)弹簧具有的最大弹性势能Epm.
(4)整个运动过程中,物体B的最大速度.
分析 (1)子弹击中木块过程系统动量守恒,对子弹和A木块构成的系统,根据动量守恒定律求解物体A被击中后的速度.
(2)分析物理过程明确弹簧拉伸至最长时,两物体的速度相同;根据动量守恒可求得B的速度;
(3)以子弹、滑块A、B和弹簧组成的系统为研究对象,当三者速度相等时,弹簧被压缩到最短,则弹性势能最大,根据动量守恒定律求出速度,然后由能量守恒定律求出弹簧的弹性势能.
(4)当弹簧再次恢复原长时,物体B达最大速度;根据动量守恒和机械能守恒可求得物体B的最大速度;
解答 解:(1)以子弹的初速度方向为正方向对子弹和A物体由动量守恒定律可知:
mv=(mA+m)vA
代入数据解得vA=20m/s;
(2)A和子弹与B组成系统动量守恒,当弹簧拉伸到最长时,AB具有相同的速度;
则由动量守恒定律可得:
mv=(mA+m+mB)vB
解得:vB=5m/s;
(3)当弹簧拉伸到最长或最短时,弹簧的弹性势能最大;
根据机械能守恒定律可得:
EPm=$\frac{1}{2}$(mA+m)vA2-$\frac{1}{2}$(mA+m+mB)v2B
解得:EPm=30J;
(4)当弹簧再次恢复原长时,mB获得速度最大,设mA速度为v1,mB速度为v2,由动量守恒定律得:
mv=mAv1+mBv2,
由机械能守恒定律得:$\frac{1}{2}$(mA+m)vA2=$\frac{1}{2}$(mA+m)v12+$\frac{1}{2}$mBv22
代入数据得:v2=10m/s;
答:(1)子弹击中A后的瞬间,物体A的速度vA为20m/s;
(2)在以后的运动过程中,弹簧被拉伸得最长时,物体B的速度vB为5m/s;
(3)弹簧具有的最大弹性势能Epm为30J;
(4)整个运动过程中,物体B的最大速度为10m/s
点评 本题考查了求速度、弹簧的弹性势能,应用动量守恒定律与能量守恒定律即可正确解题;解题时要注意,子弹击中A的过程中,子弹与A组成的系统动量守恒但机械能不守恒.

| A. | 物体的速度不变,则加速度一定为零 | |
| B. | 物体的加速度减小,则速度一定减小 | |
| C. | 物体的速度增加,则加速度可能不变 | |
| D. | 物体的速度为零时,加速度一定为零 |
| A. | 有的光是波,有的光是粒子 | |
| B. | 光子与光电子是同样的一种粒子 | |
| C. | 频率高的光的粒子性越显著,波长越长的光的波动性越显著 | |
| D. | 个别光子的行为表现出粒子性,大量光子的行为表现出波动性 |
| A. | 初速度一定为零 | B. | 只受重力作用 | ||
| C. | 加速度a=g的匀加速直线运动 | D. | 相等时间内下落高度相等 |
 如图所示,长为L的细线的一端固定于O点,另一端系一质量为m的小球.在水平拉力F作用下,小球以恒定速率在竖直平面内由最低点A运动到B点,OB与竖直方向成60°角.在此过程中( )
如图所示,长为L的细线的一端固定于O点,另一端系一质量为m的小球.在水平拉力F作用下,小球以恒定速率在竖直平面内由最低点A运动到B点,OB与竖直方向成60°角.在此过程中( )| A. | 小球所受合外力一直增大 | B. | 外力F一直增大 | ||
| C. | 小球重力势能增大$\frac{\sqrt{3}}{2}$mgL | D. | 拉力F做功为$\frac{\sqrt{3}}{2}$mgL |
 如图所示,电池组的电动势E=18V,内阻r=1Ω,R2=5Ω,R3=6Ω,平行金属板水平放置,板间距离d=2cm,当可变电阻R1的滑片移到R1的中点时,一个带电q=-8×10-7C的油滴正好平衡于平行板间,电流表示数为2A,求:
如图所示,电池组的电动势E=18V,内阻r=1Ω,R2=5Ω,R3=6Ω,平行金属板水平放置,板间距离d=2cm,当可变电阻R1的滑片移到R1的中点时,一个带电q=-8×10-7C的油滴正好平衡于平行板间,电流表示数为2A,求:
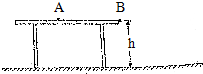 如图所示,光滑水平桌面离地高度为h=0.5m,有两个质量分别为mA=0.2kg和mB=0.3kg的小滑块用长度为l=0.5m的轻细绳相连,开始时,滑块A放在桌面上,B悬掉在桌边,细绳拉直,由静止释放,当B落地后立即被粘在地面不动,不计空气阻力和各处摩擦,g取10m/s2.试求:
如图所示,光滑水平桌面离地高度为h=0.5m,有两个质量分别为mA=0.2kg和mB=0.3kg的小滑块用长度为l=0.5m的轻细绳相连,开始时,滑块A放在桌面上,B悬掉在桌边,细绳拉直,由静止释放,当B落地后立即被粘在地面不动,不计空气阻力和各处摩擦,g取10m/s2.试求: