Question

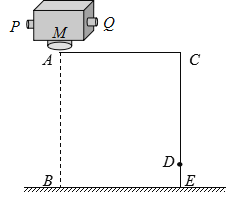
【题目】如图所示，为某月球探测器在月面软着陆的最后阶段的运动示意图。探测器原来悬停在A点，为避开正下方B处的障碍物，探测器需先水平运动到C点，再沿CD竖直下降，到达D点时速度变为0，此后探测器关闭所有发动机，在自身重力作用下自由下落至月面E点。已知月球表面重力加速度g = 1.62 m/s2，AC =1.6 m，CD = 26 m，DE = 4 m。探测器在A点时质量m = 1000 kg，从C点运动到D点所用时间为15 s。探测器主发动机M竖直向下喷气，可产生0 ~ 7500 N的变推力，辅助发动机P、Q分别水平向左、水平向右喷气，产生的推力恒为400 N，所有发动机喷出的气体相对探测器的速度大小均为u = 2000 m/s，且发动机的推力F与喷气速度u、秒流量Q（单位时间内喷出的气体质量）满足F = u·Q。探测器在如图所示的整个过程中所消耗的燃料质量Δm << m。求：

（1）探测器着陆前瞬间的速度；

（2）探测器从C点运动到D点过程中所消耗的燃料质量Δm1；

（3）探测器从A点运动到C点过程消耗的燃料质量（即喷出的气体质量）Δm2的最小值。

Answer 1

【答案】（1）3.6 m/s（2）12.15 kg （3）3.96 kg

【解析】（1）根据自由落体公式，有v2 - 0 = 2gh ①

由①式代入数据得v = 3.6 m/s ②

（2）对CD过程，根据动量定理有

IF - mgt = 0 - 0 ③

其中IF = ∑F Δt =∑u·QΔt = uΔm ④

由③④式代入数据得

Δm = 12.15 kg ⑤

（3）探测器从点运动到点的过程中，主发动机产生的推力

F1 = mg ⑥

秒流量Q1 = ⑦

发动机P或Q工作时，推力F2 = 500 N

秒流量Q2 = ⑧

发动机P或Q工作时，探测器的加速度

a = (9)

假设从A点运动到C点的过程中，探测器先加速运动t1时间，再匀速运动t2时间，最后再减速运动t3时间，易知

t1 = t3 (10)

探测器加速和减速过程中的位移

s1 = s3 =at12 ⑾

匀速过程中的位移

s2 = AC-s1-s3 ⑿

匀速运动的时间

t2 = ⒀

整个过程消耗的燃料质量

Δm2 = Q1（t1 + t2 + t3）+ Q2（t1 + t3） ⒁

由以上各式代入数据得

Δm2 = 1.21t1+ ⒂

易知，当t1==s时，Δm2最小，最小值为

Δm2min = 3.96 kg ⒃