题目内容
1.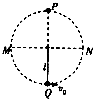 如图所示,轻绳一端系着小球在竖直平面内做圆周运动,过最低点Q时速度为v0,已知绳长为l,重力加速度为g,则( )
如图所示,轻绳一端系着小球在竖直平面内做圆周运动,过最低点Q时速度为v0,已知绳长为l,重力加速度为g,则( )| A. | 小球运动到最低点Q时,处于失重状态 | |
| B. | v0取合适值,小球运动到最高点P时,瞬时速度可减为零 | |
| C. | 速度v0越大,则在P、Q两点绳对小球的拉力差越大 | |
| D. | 当v0<$\sqrt{gl}$时,则小球运动过程中细绳始终处于绷紧状态 |
分析 小球在最高点绳子的拉力与重力的合力提供向心力,在最低点也是绳子的拉力与重力的合力提供向心力,可根据牛顿第二定律列式求解,同时小球从最高点运动得到最低点的过程中,只有重力做功,可运用动能定理列式求解.
解答 解:A、小球在最低点时.重力与拉力的合力提供向心力,所以小球受到的拉力一定大于重力,故小球处于超重状态.故A错误;
B、由于细绳不能支撑小球,所以小球运动到最高点P时,瞬时速度不可能,由mg=m$\frac{{v}^{2}}{l}$,得最高点最小速度为 v=$\sqrt{gl}$,故B错误.
C、设小球在最高点的速度为v1,最低点的速度为v2;由动能定理得:
mg(2l)=$\frac{1}{2}$m${v}_{2}^{2}$-$\frac{1}{2}$m${v}_{1}^{2}$…①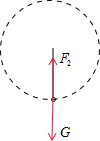 球经过最高点P:mg+F1=$\frac{m{v}_{1}^{2}}{l}$…②
球经过最高点P:mg+F1=$\frac{m{v}_{1}^{2}}{l}$…②
球经过最低点Q时,受重力和绳子的拉力,如图
根据牛顿第二定律得到,F2-mg=m$\frac{{v}_{2}^{2}}{l}$…③
联立①②③解得:F2-F1=6mg,与小球的速度v0无关.故C错误;
D、设小球恰好运动到与圆心等高位置时在最高点的速度为v,则
由机械能守恒得 mgl=$\frac{1}{2}m{v}^{2}$,v=$\sqrt{2gl}$
则v0<$\sqrt{gl}$,小球上升的最高点尚不到与圆心等高位置,所以细绳始终处于绷紧状态.故D正确.
故选:D.
点评 本题小球做变速圆周运动,在最高点和最低点重力和拉力的合力提供向心力,同时结合动能定理列式求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.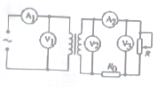 如图所示,街头变压器通过降压给用户供电,变压器的输入电压不变,输出电压通过输电线输送给用户,两条输电线的总电阻用R0表示,变阻器R代表用户用电器的总电阻,当用电器增加时,相当于R的值减少,不考虑变压器自身损耗的电能,当用户的用电器增加时( )
如图所示,街头变压器通过降压给用户供电,变压器的输入电压不变,输出电压通过输电线输送给用户,两条输电线的总电阻用R0表示,变阻器R代表用户用电器的总电阻,当用电器增加时,相当于R的值减少,不考虑变压器自身损耗的电能,当用户的用电器增加时( )
 如图所示,街头变压器通过降压给用户供电,变压器的输入电压不变,输出电压通过输电线输送给用户,两条输电线的总电阻用R0表示,变阻器R代表用户用电器的总电阻,当用电器增加时,相当于R的值减少,不考虑变压器自身损耗的电能,当用户的用电器增加时( )
如图所示,街头变压器通过降压给用户供电,变压器的输入电压不变,输出电压通过输电线输送给用户,两条输电线的总电阻用R0表示,变阻器R代表用户用电器的总电阻,当用电器增加时,相当于R的值减少,不考虑变压器自身损耗的电能,当用户的用电器增加时( )| A. | V3的读数减少 | B. | V2的读数减少 | ||
| C. | A1表的读数增大 | D. | 变压器的输入功率不变 |
10.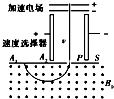 如图所示是质谱议的工作原理示意图,带电粒子被加速电场加速后,进入速度选择器,速度选择器内相互正交的匀强磁场和匀强电场的强度分别为B和E,平板S上有可让粒子通过的狭缝P和记录粒子位置的胶片A1A2,平板S下方有强度为B0的匀强磁场.下列表述正确的是( )
如图所示是质谱议的工作原理示意图,带电粒子被加速电场加速后,进入速度选择器,速度选择器内相互正交的匀强磁场和匀强电场的强度分别为B和E,平板S上有可让粒子通过的狭缝P和记录粒子位置的胶片A1A2,平板S下方有强度为B0的匀强磁场.下列表述正确的是( )
 如图所示是质谱议的工作原理示意图,带电粒子被加速电场加速后,进入速度选择器,速度选择器内相互正交的匀强磁场和匀强电场的强度分别为B和E,平板S上有可让粒子通过的狭缝P和记录粒子位置的胶片A1A2,平板S下方有强度为B0的匀强磁场.下列表述正确的是( )
如图所示是质谱议的工作原理示意图,带电粒子被加速电场加速后,进入速度选择器,速度选择器内相互正交的匀强磁场和匀强电场的强度分别为B和E,平板S上有可让粒子通过的狭缝P和记录粒子位置的胶片A1A2,平板S下方有强度为B0的匀强磁场.下列表述正确的是( )| A. | 图中运动的是带正电的粒子 | |
| B. | 速度选择器中的磁场方向垂直于纸面向内 | |
| C. | 能通过狭缝P的带电粒子的速度等于$\frac{E}{B}$ | |
| D. | 粒子打在胶片上的位置距狭缝P越远,粒子的比荷$\frac{q}{m}$越大 |
11. 发射地球同步卫星时,先将卫星发射到近地圆轨道1,然后点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3.轨道1、2相切于Q点,轨道2、3相切于P点,如图所示,则当卫星分别在1、2、3轨道上正常运行时,下列说法中正确的是( )
发射地球同步卫星时,先将卫星发射到近地圆轨道1,然后点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3.轨道1、2相切于Q点,轨道2、3相切于P点,如图所示,则当卫星分别在1、2、3轨道上正常运行时,下列说法中正确的是( )
 发射地球同步卫星时,先将卫星发射到近地圆轨道1,然后点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3.轨道1、2相切于Q点,轨道2、3相切于P点,如图所示,则当卫星分别在1、2、3轨道上正常运行时,下列说法中正确的是( )
发射地球同步卫星时,先将卫星发射到近地圆轨道1,然后点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3.轨道1、2相切于Q点,轨道2、3相切于P点,如图所示,则当卫星分别在1、2、3轨道上正常运行时,下列说法中正确的是( )| A. | 卫星在轨道3上的速率大于在轨道1上的速率 | |
| B. | 卫星在轨道3上的角速度小于在轨道1上的角速度 | |
| C. | 卫星在轨道1上经过Q点时的加速度大于它在轨道2上经过Q点时的加速度 | |
| D. | 卫星在轨道2上经过P点时的加速度小于它在轨道3上经过P点时的加速度 |
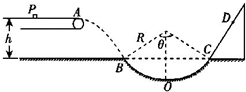 如图所示,水平传送带以一定速度匀速运动,将质量m=1kg的小物块轻轻放在传送带上的P点,物块运动到A点后被水平抛出,小物块恰好无碰撞地沿圆弧切线从B点进入竖直光滑圆弧轨道下滑.B、C为圆弧上的两点,其连线水平,已知圆弧对应圆心角θ=106°,A点距水平面的高度h=3.2m.小物块到达C点时的速度大小与B点相等,并沿固定斜面向上滑动,小物块从C点到第二次经过D点的时间间隔为1.6s,已知小物块与斜面间的动摩擦因数μ=$\frac{1}{3}$,重力加速度g取10m/s2,取sin53°=0.8,cos53°=0.6,求:
如图所示,水平传送带以一定速度匀速运动,将质量m=1kg的小物块轻轻放在传送带上的P点,物块运动到A点后被水平抛出,小物块恰好无碰撞地沿圆弧切线从B点进入竖直光滑圆弧轨道下滑.B、C为圆弧上的两点,其连线水平,已知圆弧对应圆心角θ=106°,A点距水平面的高度h=3.2m.小物块到达C点时的速度大小与B点相等,并沿固定斜面向上滑动,小物块从C点到第二次经过D点的时间间隔为1.6s,已知小物块与斜面间的动摩擦因数μ=$\frac{1}{3}$,重力加速度g取10m/s2,取sin53°=0.8,cos53°=0.6,求: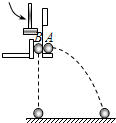 如图所示,用小锤打击弹性金属片后,A球沿水平方向抛出,同时B球被松开,自由下落,可以“听到”两球同时(填“同时”或“先后”)落地,这个实验现象能够说明A球在竖直方向做自由落体运动.
如图所示,用小锤打击弹性金属片后,A球沿水平方向抛出,同时B球被松开,自由下落,可以“听到”两球同时(填“同时”或“先后”)落地,这个实验现象能够说明A球在竖直方向做自由落体运动.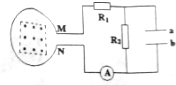 如图所示电路图,线圈的半径为40cm,线圈中边长为L=30cm的正方形内存在垂直纸面向外的匀强磁场,当匀强磁场的磁感应强度均匀增加时,平行金属板电容器的电量Q=0.1C,已知R1=8Ω,R2=10Ω,平行金属板电容器的电容为C=0.01F,线圈匝数为N=1000,电阻不计,求:
如图所示电路图,线圈的半径为40cm,线圈中边长为L=30cm的正方形内存在垂直纸面向外的匀强磁场,当匀强磁场的磁感应强度均匀增加时,平行金属板电容器的电量Q=0.1C,已知R1=8Ω,R2=10Ω,平行金属板电容器的电容为C=0.01F,线圈匝数为N=1000,电阻不计,求: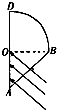 一块玻璃砖折射率为n=2,由四分之一圆柱和横截面为等腰直角三角形的棱柱组合而成,此玻璃砖的横截面如图所示,圆半径为R,一束平行光垂直AB照射到OA上,求圆弧BD上有光射出部分的弧长.
一块玻璃砖折射率为n=2,由四分之一圆柱和横截面为等腰直角三角形的棱柱组合而成,此玻璃砖的横截面如图所示,圆半径为R,一束平行光垂直AB照射到OA上,求圆弧BD上有光射出部分的弧长.