题目内容
【题目】如图所示,倾角为α的斜面体A置于粗糙水平面上,物块B置于斜面上,已知A、B的质量分别为M、m,它们之间的动摩擦因数为μ=tanα.现给B一平行于斜面向下的恒定的推力F,使B沿斜面向下运动,A始终处于静止状态,则下列说法正确的是( )
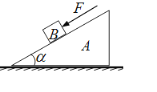
A. 无论F的大小如何,B一定加速下滑
B. B运动的加速度大小为![]()
C. 水平面对A一定有摩擦力,摩擦力方向水平向右
D. 水平面对A的支持力总是与A、B的总重力大小相等
【答案】ABD
【解析】
A、B的质量分别为M、m,它们之间的动摩擦因数为μ=tanα,可知B与A之间的摩擦力已经到达最大静摩擦力,即恰好能静止在A上,根据此结论来进行作答即可。
A、B项:由A、B之间的动摩擦因数为μ=tanα,可得:mgsinα=μmgcosα,对B进行受力分析得:F合=F,所以施加恒定的推力F后B一定加速下滑,且加速度a=![]() ,故AB正确;
,故AB正确;
C项:对B受力分析,因为μ=tanα.即B原来恰好静止在斜面上,所以斜面对B的支持力与摩擦力的合力竖直向上大小等于mg,对物体A受力分析,则B对A 的压力和摩擦力的合力由牛顿第三定律知竖直向下大小等于mg,即A水平方向没有遇到趋势,所以地面对物体A没有摩擦力。故C错误;
D项:因为B对A作用力竖直向下大小等于mg,由A竖直方向受力平衡得水平面对A的支持力总是与A、B的总重力大小相等,故D正确。
故选:ABD。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目