题目内容
如图甲所示,在直角坐标系0≤x≤L区域内有沿y轴正方向的匀强电场,右侧有个以点(3L,0)为圆心,半径为L的圆形区域,圆形区域与x轴的交点分别为M、N.现有一质量为m,带电量为ec的电子,从y轴上的A点以速度v0沿x轴正方向射入电场,飞出电场后恰能从M点进入圆形区域,速度方向与x轴夹角为30°,电子从M点射入的瞬间在圆形区域加如图乙所示周期性变化的磁场(磁场从t=0时刻开始变化,且以垂直于纸面向外为正方向),电子运动一段时间后从N点飞出,速度方向与x轴夹角也为30°.求:
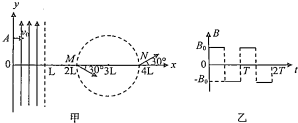
(1)0≤x≤L区域内匀强电场的场强大小;
(2)A点的纵坐标yA;
(3)磁场的磁感应强度B.的可能值及磁场的变化周期T.

(1)0≤x≤L区域内匀强电场的场强大小;
(2)A点的纵坐标yA;
(3)磁场的磁感应强度B.的可能值及磁场的变化周期T.
(1)电子在电场中做类平抛运动,运动轨迹如图所示,由速度关系得:由速度关系解得vy=v0tan30°
水平方向:L=v0t
竖直方向:vy=
| eE |
| m |
联立解得,E=
| ||||
| 3eL |
(2)电子在电场中做类平抛运动过程,
y1=
| 1 |
| 2 |
| eE |
| m |
电子飞出电场运动到M的过程中做匀速直线运动,则
y2=Ltan30°
故A点的纵坐标yA=y1+y2=
| ||
| 2 |
(3)电子进入磁场时的速度为
v=
| v0 |
| cos30° |
2
| ||
| 3 |
电子在磁场中运动的轨迹如图乙所示,则几何知识得
(2n+1)R=2L(n=0,1,2,…)
电子在磁场中由洛伦兹力提供向心力,由牛顿第二定律得
evB0=m
| v2 |
| R |
解得,B0=
(2n+1)
| ||
| 3eL |
电子在磁场中运动的周期为 T′=
| 2πm |
| eB0 |
由题意得:
| T |
| 2 |
| T′ |
| 6 |
解得,T=
2
| ||
| 3(2n+1)v0 |
(1)0≤x≤L区域内匀强电场的场强大小是
| ||||
| 3eL |
(2)A点的纵坐标yA是
| ||
| 2 |
(3)磁场的磁感应强度B的可能值
(2n+1)
| ||
| 3eL |
2
| ||
| 3(2n+1)v0 |

练习册系列答案
相关题目
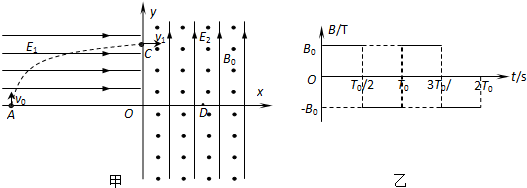

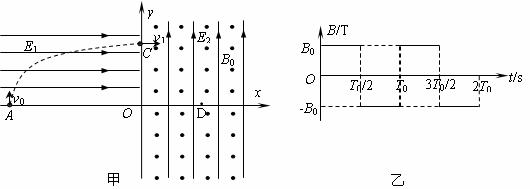
 ,匀强磁场方向垂直纸面。处在第三象限的某种发射装置(图中没有画出)竖直向上射出一个比荷
,匀强磁场方向垂直纸面。处在第三象限的某种发射装置(图中没有画出)竖直向上射出一个比荷 的带正电的微粒(可视为质点),该微粒以v0=4m/s的速度从-x上的A点进入第二象限,并以v1=8m/s速度从+y上的C点沿水平方向进入第一象限。取微粒刚进入第一象限的时刻为0时刻,磁感应强度按图乙所示规律变化(以垂直纸面向外的磁场方向为正方向),g="10" m/s2.试求:
的带正电的微粒(可视为质点),该微粒以v0=4m/s的速度从-x上的A点进入第二象限,并以v1=8m/s速度从+y上的C点沿水平方向进入第一象限。取微粒刚进入第一象限的时刻为0时刻,磁感应强度按图乙所示规律变化(以垂直纸面向外的磁场方向为正方向),g="10" m/s2.试求:
 角。当θ =37°时,(g = 9.8m/s2,sin37°= 0.6,cos37°= 0.8)求:
角。当θ =37°时,(g = 9.8m/s2,sin37°= 0.6,cos37°= 0.8)求: